by minkwe » Wed Sep 06, 2023 12:31 pm
FrediFizzx wrote: ↑Wed Sep 06, 2023 11:51 am
Well, thanks but it doesn't resolve the dispute. Joy claims the singlet spin vector, "s", above is a hidden variable. I say it is not a hidden variable since quantum mechanics knows about it via the singlet wavefunction. What say you?
What we have here is two different local EPR-Bohm models that give the prediction of quantum mechanics with NO hidden variables. One is a classical type of model the other is a quantum mechanical model.
.
I say as far as Bell's theorem is concerned, "hidden variables" used to mean "additional variables added to the quantum-mechanical description" are irrelevant. As I explained above, the variables in Bell's theorem are not "hidden variables", although they may include hidden variables. If someone is able to demonstrate that A(a, s) reproduces the correlations and deterministically produces individual outcomes, whatever you call "s", then "s" must be a more complete description of reality. If "s" is ONLY the quantum-mechanical description without any additional variables, then EPR and Bell both don't think that is possible. As bell further explains:
Bell 1964 wrote:With the example advocated by Bohm and Aharonov [6], the EPR argument is the following. Consider a pair of spin one-half particles formed somehow in the singlet spin state and moving freely in opposite directions. Measurements can be made, say by Stern-Gerlach magnets, on selected components of the Spins
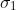
and
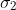
. If measurement Of the component
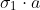
, where
a is some unit vector, yields the value + 1 then, according to quantum mechanics, measurement of
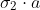
must yield the value -1 and vice versa.
Now we make the hypothesis [2], and it seems at least worth considering that if the two measurements are made at places remote from one another, the orientation of one magnet does not influence the result obtained with the other. Since we can predict in advance the result of measuring any chosen component of
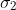
by previously measuring the same component of
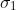
, it follows that the result of any such measurement must actually be predetermined.
Since the initial quantum mechanical wave function does not determine the result of an individual measurement, this predetermination implies the possibility of a more complete specification of the state.
Note that here, simply reproducing the QM correlations is not enough to fulfill the requirements laid out by Bell. The model must be able to produce the results of individual measurements deterministically.
Secondly, the idea that you have a different EPR-Bohm model that gives the prediction of QM with "NO hidden variables" is also meaningless. Once you start dealing with a completely different theory than quantum mechanics, then the concept of "hidden variables," understood to mean "variables added to QM to complete it", is meaningless since they refer only to the variables required to "expand" the quantum-mechanical description.
On the other hand, if you have adopted the recent trend where λ in Bell's A(a λ) is casually referred to as "hidden variables," then nitpicking about whether "s" is a hidden variable or not is a waste of time because it obviously is (according to this view) if your functions are A(a, s). Also, according to this view, the idea that anything can reproduce the correlations without any hidden variables is also meaningless unless your functions are A(a). In this case, all particles are identical (obviously false), and the outcomes are always identical for the same angle for every experiment (obviously false).
[quote=FrediFizzx post_id=975 time=1694026263 user_id=58]
Well, thanks but it doesn't resolve the dispute. Joy claims the singlet spin vector, "s", above is a hidden variable. I say it is not a hidden variable since quantum mechanics knows about it via the singlet wavefunction. What say you?
What we have here is two different local EPR-Bohm models that give the prediction of quantum mechanics with NO hidden variables. One is a classical type of model the other is a quantum mechanical model.
.
[/quote]
I say as far as Bell's theorem is concerned, "hidden variables" used to mean "additional variables added to the quantum-mechanical description" are irrelevant. As I explained above, the variables in Bell's theorem are not "hidden variables", although they may include hidden variables. If someone is able to demonstrate that A(a, s) reproduces the correlations and deterministically produces individual outcomes, whatever you call "s", then "s" must be a more complete description of reality. If "s" is ONLY the quantum-mechanical description without any additional variables, then EPR and Bell both don't think that is possible. As bell further explains:
[quote="Bell 1964"]With the example advocated by Bohm and Aharonov [6], the EPR argument is the following. Consider a pair of spin one-half particles formed somehow in the singlet spin state and moving freely in opposite directions. Measurements can be made, say by Stern-Gerlach magnets, on selected components of the Spins [tex]\sigma_1[/tex] and [tex]\sigma_2[/tex]. If measurement Of the component [tex]\sigma_1 \cdot a[/tex], where [i]a[/i] is some unit vector, yields the value + 1 then, according to quantum mechanics, measurement of [tex]\sigma_2 \cdot a[/tex] must yield the value -1 and vice versa.
Now we make the hypothesis [2], and it seems at least worth considering that if the two measurements are made at places remote from one another, the orientation of one magnet does not influence the result obtained with the other. Since we can predict in advance the result of measuring any chosen component of [tex]\sigma_2[/tex] by previously measuring the same component of[tex]\sigma_1[/tex], it follows that the result of any such measurement must actually be predetermined. [b]Since the initial quantum mechanical wave function does not determine the result of an individual measurement, this predetermination implies the possibility of a more complete specification of the state.[/b][/quote]
Note that here, simply reproducing the QM correlations is not enough to fulfill the requirements laid out by Bell. The model must be able to produce the results of individual measurements deterministically.
Secondly, the idea that you have a different EPR-Bohm model that gives the prediction of QM with "NO hidden variables" is also meaningless. Once you start dealing with a completely different theory than quantum mechanics, then the concept of "hidden variables," understood to mean "variables added to QM to complete it", is meaningless since they refer only to the variables required to "expand" the quantum-mechanical description.
On the other hand, if you have adopted the recent trend where λ in Bell's A(a λ) is casually referred to as "hidden variables," then nitpicking about whether "s" is a hidden variable or not is a waste of time because it obviously is (according to this view) if your functions are A(a, s). Also, according to this view, the idea that anything can reproduce the correlations without any hidden variables is also meaningless unless your functions are A(a). In this case, all particles are identical (obviously false), and the outcomes are always identical for the same angle for every experiment (obviously false).
