Sci.Physics.Foundations

gill1109 wrote: ↑Sun Nov 14, 2021 9:20 pm ... In Tsirelson’s mathematical proof of his famous inequality, the four terms are not independent. They depend on the same four observables (self-adjoint operators) A, A’, B, B’ and the same quantum state rho on the same Hilbert space H.

When Tsirelson’s observables commute, his model is fully equivalent to Bell’s model. Four commuting observables correspond to four Kolmogorovian random variables, and vice versa. ...

Pure nonsense. The terms might not be completely independent but there is no way in hell that the dependency is the same as Bell's.
.

FrediFizzx wrote: ↑Mon Nov 15, 2021 4:14 am

gill1109 wrote: ↑Sun Nov 14, 2021 9:20 pm ... In Tsirelson’s mathematical proof of his famous inequality, the four terms are not independent. They depend on the same four observables (self-adjoint operators) A, A’, B, B’ and the same quantum state rho on the same Hilbert space H.

When Tsirelson’s observables commute, his model is fully equivalent to Bell’s model. Four commuting observables correspond to four Kolmogorovian random variables, and vice versa. ...

Pure nonsense. The terms might not be completely independent but there is no way in hell that the dependency is the same as Bell's.

If in Tsirelson’s case you would restrict yourself to four commuting observables, you would get the same bound as Bell did.

The Tsirelson bound has four observables such that A and A’ each commute with each of B and B’. But A need not commute with A’, and B need not commute with B’.

Bell’s bound has four observables A, A’, B, B’ all commuting with one another.

Both allow an arbitrary quantum state on an arbitrary Hilbert space.

All observables are restricted to take values (when observed) -1 and +1 only.

Tsirelson maximises over a strictly larger space of possibilities than Bell, and not surprisingly, finds a bigger supremum. Tsirelson even shows that his bound is *uniquely* attained by a quantum state and four observables isomorphic to the usual EPR-B solution.

All these mathematical facts have been well known for more than 40 years.

@gill1109 Nonsense that you have used to brainwash yourself for more than 40 years.
.

FrediFizzx wrote: ↑Tue Nov 16, 2021 4:06 am @gill1109 Nonsense that you have used to brainwash yourself for more than 40 years.

Do you mean that maths is nonsense?

I went up to Cambridge in 1974 to study physics, treading in the footsteps of my father. I joined Gonville and Caius College, the college of R.A. Fisher and John Venn. After one year I switched to mathematics since the physics lectures just wanted you to absorb the dogmas of physicists of the past. The mathematicians, like J.H. Conway, forced you to *think*. The supervision by Stephen Hawking put me off differential equations for life.

gill1109 wrote: ↑Tue Nov 16, 2021 5:38 am

FrediFizzx wrote: ↑Tue Nov 16, 2021 4:06 am @gill1109 Nonsense that you have used to brainwash yourself for more than 40 years.

Do you mean that maths is nonsense?

I went up to Cambridge in 1974 to study physics, treading in the footsteps of my father. I joined Gonville and Caius College, the college of R.A. Fisher and John Venn. After one year I switched to mathematics since the physics lectures just wanted you to absorb the dogmas of physicists of the past. The mathematicians, like J.H. Conway, forced you to *think*. The supervision by Stephen Hawking put me off differential equations for life.

Hmm.... I think we found your problem.
.

FrediFizzx wrote: ↑Tue Nov 16, 2021 7:14 am

gill1109 wrote: ↑Tue Nov 16, 2021 5:38 am

FrediFizzx wrote: ↑Tue Nov 16, 2021 4:06 am @gill1109 Nonsense that you have used to brainwash yourself for more than 40 years.

Do you mean that maths is nonsense?

I went up to Cambridge in 1974 to study physics, treading in the footsteps of my father. I joined Gonville and Caius College, the college of R.A. Fisher and John Venn. After one year I switched to mathematics since the physics lectures just wanted you to absorb the dogmas of physicists of the past. The mathematicians, like J.H. Conway, forced you to *think*. The supervision by Stephen Hawking put me off differential equations for life.

Hmm.... I think we found your problem.

That was before Hawking had his speech computer. He sat in a wheelchair hunched up, leaning over the table top, drooling, making indecipherable noises, and making scratch-marks on a notepad with a ball-pen. It was utterly traumatic. My three or four fellow students were aged about 20. Young kids from the provinces, basically. Cambridge is an utterly weird place anyway. I have all respect for Hawking’s tenacity and for his intellect. Though, when I read that book with a debate between him and Penrose, I think that Penrose has a much sharper mind.

@gill1109 Yep, we found your problem!
.

My problem was the physicists’ attitude “shut up and calculate”. Don’t ask questions. Just watch how we do it, and copy that. The mathematicians’ attitude was: find out *why* a certain weird looking calculation does work. Keep on asking questions. Find deep connections between seemingly unrelated parts of mathematics. Always question the assumptions which you make without thinking, for convenience’ sake and because everyone else does.

gill1109 wrote: ↑Thu Nov 18, 2021 7:59 pm My problem was the physicists’ attitude “shut up and calculate”. Don’t ask questions. Just watch how we do it, and copy that. The mathematicians’ attitude was: find out *why* a certain weird looking calculation does work. Keep on asking questions. Find deep connections between seemingly unrelated parts of mathematics. Always question the assumptions which you make without thinking, for convenience’ sake and because everyone else does.

Yeah, yeah, yeah, blame it on somebody.
.

FrediFizzx wrote: ↑Thu Nov 18, 2021 8:08 pm

gill1109 wrote: ↑Thu Nov 18, 2021 7:59 pm My problem was the physicists’ attitude “shut up and calculate”. Don’t ask questions. Just watch how we do it, and copy that. The mathematicians’ attitude was: find out *why* a certain weird looking calculation does work. Keep on asking questions. Find deep connections between seemingly unrelated parts of mathematics. Always question the assumptions which you make without thinking, for convenience’ sake and because everyone else does.

Yeah, yeah, yeah, blame it on somebody.

I'm not blaming anything on anybody. I think that in science, we need mathematicians and physicists. Nobody should underestimate what the other way of thinking has to offer. One must learn to communicate and to appreciate.

Since so far *nobody* has actually responded to the original post, I will repeat it here.

It's about a little exercise in elementary probability theory which I published in several papers more than 20 years ago, and recently, again, in my published "Comments" on some papers by Joy Christian in IEEE Access and in RSOS.

So far, only @minkwe entered the mathematics discussion, but he did this by talking about a different proof of a quite different claim.

Here it goes again:

Let be four random variables taking the values
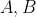
Let be two random variables taking the values
Suppose is statistically independent of
Define and
In other words, if , if ; if , if
Define

Theorem: lies in the interval .

Proof:

can only take the values

Hence
lies in .

But by statistical independence of from
because when
.

QED

I claim that this theorem is useful in the analysis of classical computer simulation of quantum correlations. It tells us that in order to achieve your aim, you will have to violate the conditions of the theorem. Obviously, there are very many ways to do this!

@gill1109 "Obviously, there are very many ways to do this!" ??? Then what you are claiming as a theorem is not a theorem but just a theory.
.

FrediFizzx wrote: ↑Sat Nov 20, 2021 7:10 am @gill1109 "Obviously, there are very many ways to do this!" ??? Then what you are claiming as a theorem is not a theorem but just a theory.

It's a mathematical theorem. I say that if A, B, C, D and E all hold, then F is true as well. I simply do not discuss the many ways you can avoid the conclusions of the theorem. The theorem has a number of assumptions. You can avoid the conclusions by violating some or all of the assumptions.

Joy Christian has tried several different ways in his papers.

You could:

Relax the assumption that outcomes are binary
Alter your definition of correlation
Violate locality
Violate no-conspiracy (statistical independence)
Violate realism

I do not say that A, B, C, D and E are true if and only if F is true.

Fine has a theorem giving necessary and sufficient conditions for the 8 one-sided CHSH inequalities (but still assuming some background assumptions); Boole did the same (in retrospect) for the 6 one-sided original Bell inequalities.

@gill1109 You've got no theorem. All you have is a junk math theory. Stop spewing nonsense like the above!
.

I presented a mathematical theorem. It uses the standard notation and concepts of probability theory. If you don’t know them, you might have difficulties reading what I wrote. Ask questions. Let me know what you don’t understand.

gill1109 wrote: ↑Mon Nov 22, 2021 9:26 pm I presented a mathematical theorem. It uses the standard notation and concepts of probability theory. If you don’t know them, you might have difficulties reading what I wrote. Ask questions. Let me know what you don’t understand.

Now that is really funny because I don't think I have ever seen you do,

Theorem 1: Blah, Blah, Blah, ....

IOW, I don't think I have ever seen you make a real theorem statement like they do in most math documents. Send me a link if you have.
.

FrediFizzx wrote: ↑Wed Nov 24, 2021 7:10 am

gill1109 wrote: ↑Mon Nov 22, 2021 9:26 pm I presented a mathematical theorem. It uses the standard notation and concepts of probability theory. If you don’t know them, you might have difficulties reading what I wrote. Ask questions. Let me know what you don’t understand.

Now that is really funny because I don't think I have ever seen you do,
Theorem 1: Blah, Blah, Blah, ....
IOW, I don't think I have ever seen you make a real theorem statement like they do in most math documents. Send me a link if you have.

Take a look at my Theorem 1 in https://arxiv.org/abs/1207.5103
Statistics, Causality and Bell's Theorem

Abstract: Bell's [Physics 1 (1964) 195-200] theorem is popularly supposed to establish the nonlocality of quantum physics. Violation of Bell's inequality in experiments such as that of Aspect, Dalibard and Roger [Phys. Rev. Lett. 49 (1982) 1804-1807] provides empirical proof of nonlocality in the real world. This paper reviews recent work on Bell's theorem, linking it to issues in causality as understood by statisticians. The paper starts with a proof of a strong, finite sample, version of Bell's inequality and thereby also of Bell's theorem, which states that quantum theory is incompatible with the conjunction of three formerly uncontroversial physical principles, here referred to as locality, realism and freedom. Locality is the principle that the direction of causality matches the direction of time, and that causal influences need time to propagate spatially. Realism and freedom are directly connected to statistical thinking on causality: they relate to counterfactual reasoning, and to randomisation, respectively. Experimental loopholes in state-of-the-art Bell type experiments are related to statistical issues of post-selection in observational studies, and the missing at random assumption. They can be avoided by properly matching the statistical analysis to the actual experimental design, instead of by making untestable assumptions of independence between observed and unobserved variables. Methodological and statistical issues in the design of quantum Randi challenges (QRC) are discussed. The paper argues that Bell's theorem (and its experimental confirmation) should lead us to relinquish not locality, but realism.

Statistical Science 2014, Vol. 29, No. 4, 512-528
DOI: 10.1214/14-STS490

Theorem 1. Given an N × 4 spreadsheet of numbers ±1 with columns A, A′, B and B′, suppose that, completely at random, just one of A and A′ is observed and just one of B and B′ are observed in every row. Then, for any η ≥ 0, (3) [displayed equation].

The various objects defined in equation (3) are defined earlier in the paper. I will see if I can put the equation into this thread later on, as well as the needed definitions.

The proof is given in full later in the paper.

Ha, got it.



Here, <AB>_{obs} stands for the average of the products of what is in columns A and B, over just those rows where A and B were both selected for observation. In each row, either A or A' is selected, and B or B' is selected, each with probability a half. All 2N selections independent of one another.

How to use the theorem. For instance you want to know how large N should be such that the chance that the CHSH-like quantity in the theorem is smaller than 2.1 with probability 99%. Then find the value of N such that, with eta = 0.1, 8 exp( - N (eta/16)^2 ) = 0.01

gill1109 wrote: ↑Wed Nov 24, 2021 9:31 am How to use the theorem. For instance you want to know how large N should be such that the chance that the CHSH-like quantity in the theorem is smaller than 2.1 with probability 99%. Then find the value of N such that, with eta = 0.1, 8 exp( - N (eta/16)^2 ) = 0.01

So, like this?



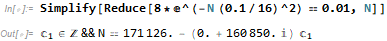
Then N = 171126 minus some imaginary number? What the heck does that tell us?

But it matters not because this kills it all.

https://www.wolframcloud.com/obj/fredif ... c-forum.nb

Like I was saying, you got NO proof anymore!
.
PS. Which means you can stop posting your nonsense any time now!
.