Page 2 of 5
Re: Superdeterminism
Posted: Sun Dec 26, 2021 10:54 am
by minkwe
Joy Christian wrote: ↑Sun Dec 26, 2021 9:16 am
minkwe wrote: ↑Sun Dec 26, 2021 8:13 am
FrediFizzx wrote: ↑Sat Dec 25, 2021 6:59 pm
I'm sorry, but that statement sound a bit "fishy" to me. If p(h) originates with the source, then I really don't see how it could depend on both "a" and "b". Those vectors have not even happened yet!
.
I don't think you guys are understanding me. I suspect that Richard understands but as usual he wants to play games because I've explained this to him before and he started scrambling to find a disingenuous way out.
Okay Fred, let us do a little exercise. Let

,
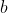
and
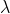
be vectors. Forget for a moment what those vectors mean physically. Focus on the maths.
 = -B(a, \lambda) = \frac{1}{-sign(a \cdot \lambda)})
 = A(a,\lambda)B(b, \lambda))
What is the domain of
)
, what is the domain of
)
, what is the domain of
)
I understand what you are saying. No technical discussion is necessary to understand the issue. It has been known and discussed extensively for the past fifty years. There are two options for the derivations of Bell inequalities:
(a) the probability distribution p(h) is independent of the settings a and b. This has been assumed by Bell to derive the bound of 2 on CHSH.
(b) the probability distribution depends on the settings a and b so that p(a, b|h) =/= p(h). This is the assumption of "superdeterminism."
So the options are clear cut. With option (b) the bound of 2 on CHSH cannot be derived. Therefore one can construct a locally causal theory.
The only remaining questions are: (i) What does option (b) mean physically and conceptually? And (ii): What price one must pay for the option (b).
.
Please answer my question in the previous post.
Re: Superdeterminism
Posted: Sun Dec 26, 2021 11:03 am
by Joy Christian
minkwe wrote: ↑Sun Dec 26, 2021 10:54 am
Joy Christian wrote: ↑Sun Dec 26, 2021 9:16 am
minkwe wrote: ↑Sun Dec 26, 2021 8:13 am
I don't think you guys are understanding me. I suspect that Richard understands but as usual he wants to play games because I've explained this to him before and he started scrambling to find a disingenuous way out.
Okay Fred, let us do a little exercise. Let

,
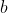
and
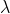
be vectors. Forget for a moment what those vectors mean physically. Focus on the maths.
 = -B(a, \lambda) = \frac{1}{-sign(a \cdot \lambda)})
 = A(a,\lambda)B(b, \lambda))
What is the domain of
)
, what is the domain of
)
, what is the domain of
)
I understand what you are saying. No technical discussion is necessary to understand the issue. It has been known and discussed extensively for the past fifty years. There are two options for the derivations of Bell inequalities:
(a) the probability distribution p(h) is independent of the settings a and b. This has been assumed by Bell to derive the bound of 2 on CHSH.
(b) the probability distribution depends on the settings a and b so that p(a, b|h) =/= p(h). This is the assumption of "superdeterminism."
So the options are clear cut. With option (b) the bound of 2 on CHSH cannot be derived. Therefore one can construct a locally causal theory.
The only remaining questions are: (i) What does option (b) mean physically and conceptually? And (ii): What price one must pay for the option (b).
Please answer my question in the previous post.
The answers are trivial. The domain of A is (a, h), the domain of B is (b, h), and the domain of C is (a, b, h). So what? What do they mean physically?
.
Re: Superdeterminism
Posted: Sun Dec 26, 2021 11:07 am
by minkwe
Joy Christian wrote: ↑Sun Dec 26, 2021 9:16 am
(a) the probability distribution p(h) is independent of the settings a and b. This has been assumed by Bell to derive the bound of 2 on CHSH.
(b) the probability distribution depends on the settings a and b so that p(a, b|h) =/= p(h). This is the assumption of "superdeterminism."
So the options are clear cut. With option (b) the bound of 2 on CHSH cannot be derived. Therefore one can construct a locally causal theory.
The only remaining questions are: (i) What does option (b) mean physically and conceptually? And (ii): What price one must pay for the option (b).
.
I'm explaining to you guys what option (b) means conceptually. I'm explaining that option (b) does is not necessarily absurd or involves such concepts as retrocausality of loss of freedom that most people immediately assume. Physically, there are several possibilities non-absurd possibilities that arise once the conceptual explanation is understood.
Re: Superdeterminism
Posted: Sun Dec 26, 2021 11:32 am
by FrediFizzx
minkwe wrote: ↑Sun Dec 26, 2021 11:07 am
Joy Christian wrote: ↑Sun Dec 26, 2021 9:16 am
(a) the probability distribution p(h) is independent of the settings a and b. This has been assumed by Bell to derive the bound of 2 on CHSH.
(b) the probability distribution depends on the settings a and b so that p(a, b|h) =/= p(h). This is the assumption of "superdeterminism."
So the options are clear cut. With option (b) the bound of 2 on CHSH cannot be derived. Therefore one can construct a locally causal theory.
The only remaining questions are: (i) What does option (b) mean physically and conceptually? And (ii): What price one must pay for the option (b).
.
I'm explaining to you guys what option (b) means conceptually. I'm explaining that option (b) does is not necessarily absurd or involves such concepts as retrocausality of loss of freedom that most people immediately assume. Physically, there are several possibilities non-absurd possibilities that arise once the conceptual explanation is understood.
Well, you need to explain it better because it makes NO sense to me.
.
Re: Superdeterminism
Posted: Sun Dec 26, 2021 11:50 am
by minkwe
Joy Christian wrote: ↑Sun Dec 26, 2021 11:03 am
The answers are trivial. The domain of A is (a, h), the domain of B is (b, h), and the domain of C is (a, b, h). So what? What do they mean physically?
You dismiss the question, but the answer is not what you state.
The domain of A(a,h) for the function I gave is not just (a,h). it is (a, h) but only those values of "a" and "h" where where "a" is not orthogonal to "h". And for B(b, h), it is (b, h) except for the region where "b" is orthogonal to "h". For C(a, b, h), it is (a, b, h) except for the regions where either "a" is orthogonal to "h" or "b" is orthogonal to "h".
Already from this simple function p(h) =/= p(h|a) =/= p(h|b) =/= p(h|a,b). Which is essentially the definition of so-called "superdeterminism".
Perhaps what you are wondering is what does a function like A(a,h) = -1/sign(a.h) mean physically. That's an interesting question. But I never heard anyone explain what Bell's equation (4) from his original paper meant physically. My function above is more true to Bell's original intent in his equation (1). In equation (1), he writes that
A(a, h) = +/- 1
The function takes two vectors which if considered unit vectors, can be thought of as points on a sphere (ie, you can represent any two vectors with their bi-vector, which is homeomorphic with the normal of the plane defined by the two vectors, and points on the sphere can be used to represent all unit vectors on the sphere). He then maps those points to two integers (+1, -1).
This is similar to a game in which we try to color the surface of a sphere using two colours only. Functions satisfying Bell's equation (1) are functions that try to do such colouring. The fact that for A(a,h) = -1/sign(a.h), p(h) =/= p(h|a) simply means that there is a circle on this sphere (the boundary between the two colors where no color can be assigned.
What color will your model assign when "a" is orthogonal to "h"?
Re: Superdeterminism
Posted: Sun Dec 26, 2021 12:07 pm
by Joy Christian
.
Bell's eq. (4) makes perfect mathematical and physical sense. The sign function simply picks out a normalized component of the spin vector, his lambda in eq. (4), about the detector vector a, representing a scalar point +/-1 on a unit 2-sphere. That is analogous to what happens in a Stern–Gerlach apparatus.
.
Re: Superdeterminism
Posted: Sun Dec 26, 2021 12:22 pm
by minkwe
Joy Christian wrote: ↑Sun Dec 26, 2021 12:07 pm
.
Bell's eq. (4) makes perfect mathematical and physical sense. The sign function simply picks out a normalized component of the spin vector, his lambda in eq. (4), about the detector vector
a, representing a scalar point +/-1 on a unit 2-sphere. That is analogous to what happens in a Stern–Gerlach apparatus.
.
Then you should not be surprised what A(a,h) = 1/sign(a.h) means physically. But wait, what scalar point does Bell's equation (4) give when those two vectors ("a", "h") are orthogonal?
Re: Superdeterminism
Posted: Sun Dec 26, 2021 12:25 pm
by FrediFizzx
minkwe wrote: ↑Sun Dec 26, 2021 12:22 pm
Joy Christian wrote: ↑Sun Dec 26, 2021 12:07 pm
.
Bell's eq. (4) makes perfect mathematical and physical sense. The sign function simply picks out a normalized component of the spin vector, his lambda in eq. (4), about the detector vector
a, representing a scalar point +/-1 on a unit 2-sphere. That is analogous to what happens in a Stern–Gerlach apparatus.
.
Then you should not be surprised what A(a,h) = 1/sign(a.h) means physically. But wait, what scalar point does Bell's equation (4) give when those two vectors ("a", "h") are orthogonal?
You are assuming "h" is a vector. What if it is just a scalar?
Re: Superdeterminism
Posted: Sun Dec 26, 2021 12:33 pm
by Joy Christian
minkwe wrote: ↑Sun Dec 26, 2021 12:22 pm
Joy Christian wrote: ↑Sun Dec 26, 2021 12:07 pm
.
Bell's eq. (4) makes perfect mathematical and physical sense. The sign function simply picks out a normalized component of the spin vector, his lambda in eq. (4), about the detector vector
a, representing a scalar point +/-1 on a unit 2-sphere. That is analogous to what happens in a Stern–Gerlach apparatus.
.
Then you should not be surprised what A(a,h) = 1/sign(a.h) means physically. But wait, what scalar point does Bell's equation (4) give when those two vectors ("a", "h") are orthogonal?
If a happens to be orthogonal to h (the measure of that happening, by the way, is nearly zero), then sign(h.a) is assumed to be equal to the sign of the first nonzero component from the set {a_x, a_y, a_z}. Bell does not specify this in his 1964 paper, but he does so in a later paper, and so do GHSZ in their paper.
.
Re: Superdeterminism
Posted: Sun Dec 26, 2021 1:11 pm
by minkwe
FrediFizzx wrote: ↑Sun Dec 26, 2021 12:25 pm
minkwe wrote: ↑Sun Dec 26, 2021 12:22 pm
Joy Christian wrote: ↑Sun Dec 26, 2021 12:07 pm
.
Bell's eq. (4) makes perfect mathematical and physical sense. The sign function simply picks out a normalized component of the spin vector, his lambda in eq. (4), about the detector vector
a, representing a scalar point +/-1 on a unit 2-sphere. That is analogous to what happens in a Stern–Gerlach apparatus.
.
Then you should not be surprised what A(a,h) = 1/sign(a.h) means physically. But wait, what scalar point does Bell's equation (4) give when those two vectors ("a", "h") are orthogonal?
You are assuming "h" is a vector. What if it is just a scalar?
.
It is a vector for the function I provided. I'm allowed to define "h" that way according to Bell.
Re: Superdeterminism
Posted: Sun Dec 26, 2021 1:28 pm
by minkwe
Joy Christian wrote: ↑Sun Dec 26, 2021 12:33 pm
minkwe wrote: ↑Sun Dec 26, 2021 12:22 pm
Then you should not be surprised what A(a,h) = 1/sign(a.h) means physically. But wait, what scalar point does Bell's equation (4) give when those two vectors ("a", "h") are orthogonal?
If a happens to be orthogonal to h (the measure of that happening, by the way, is nearly zero), then sign(h.a) is assumed to be equal to the sign of the first nonzero component from the set {a_x, a_y, a_z}. Bell does not specify this in his 1964 paper, but he does so in a later paper, and so do GHSZ in their paper.
.
Bell's function is A(a, h) = sign(a.h). What you describe above is a different function. I'm not sure this function containing "the sign of the first nonzero component from the set {a_x, a_y, a_z}" still makes perfect mathematical and physical sense?
(the measure of that happening, by the way, is nearly zero)
Nearly zero is not the same as zero. Besides, I picked the most trivial example to illustrate this point. It is possible to construct more elaborate functions for which the measure is not as small as you think. The point is that we can arrive at p(h) =/= p(h|a) =/= p(h|ab) for the type of function I gave without anything spooky.
Re: Superdeterminism
Posted: Sun Dec 26, 2021 1:37 pm
by FrediFizzx
minkwe wrote: ↑Sun Dec 26, 2021 1:11 pm
FrediFizzx wrote: ↑Sun Dec 26, 2021 12:25 pm
minkwe wrote: ↑Sun Dec 26, 2021 12:22 pm
Then you should not be surprised what A(a,h) = 1/sign(a.h) means physically. But wait, what scalar point does Bell's equation (4) give when those two vectors ("a", "h") are orthogonal?
You are assuming "h" is a vector. What if it is just a scalar?
.
It is a vector for the function I provided. I'm allowed to define "h" that way according to Bell.
You didn't answer my question. What if "h" is a scalar?
.
Re: Superdeterminism
Posted: Sun Dec 26, 2021 1:43 pm
by Joy Christian
minkwe wrote: ↑Sun Dec 26, 2021 1:28 pm
Joy Christian wrote: ↑Sun Dec 26, 2021 12:33 pm
minkwe wrote: ↑Sun Dec 26, 2021 12:22 pm
Then you should not be surprised what A(a,h) = 1/sign(a.h) means physically. But wait, what scalar point does Bell's equation (4) give when those two vectors ("a", "h") are orthogonal?
If a happens to be orthogonal to h (the measure of that happening, by the way, is nearly zero), then sign(h.a) is assumed to be equal to the sign of the first nonzero component from the set {a_x, a_y, a_z}. Bell does not specify this in his 1964 paper, but he does so in a later paper, and so do GHSZ in their paper.
.
Bell's function is A(a, h) = sign(a.h). What you describe above is a different function. I'm not sure this function containing "the sign of the first nonzero component from the set {a_x, a_y, a_z}" still makes perfect mathematical and physical sense?
(the measure of that happening, by the way, is nearly zero)
Nearly zero is not the same as zero.
The probability of h.a = 0 occurring in any real experiment is zero. But the special prescription I specified above for the case h.a = 0 eliminates that accidental possibility and makes sure that all results A = sign(h.a) are always nonzero. There are no zero or discarded results. No detection loophole.
I remain unconvinced that assuming setting dependent probability distribution of hidden variables makes physical sense. We are not doing mathematics.
.
Re: Superdeterminism
Posted: Sun Dec 26, 2021 1:59 pm
by minkwe
FrediFizzx wrote: ↑Sun Dec 26, 2021 1:37 pm
minkwe wrote: ↑Sun Dec 26, 2021 1:11 pm
FrediFizzx wrote: ↑Sun Dec 26, 2021 12:25 pm
You are assuming "h" is a vector. What if it is just a scalar?
.
It is a vector for the function I provided. I'm allowed to define "h" that way according to Bell.
You didn't answer my question. What if "h" is a scalar?
.
then 1/sign(a.h) makes no sense since the dot product is meaningless for a scalar. Not sure what you are getting at though. The function I gave is for vectors, just like the one Bell gave also. I could envision another trivial case where both "a" and "h" are scalars, and A(a,h) -B(a, h) = -1/sign(a-h). In this case, we have exactly the same thing.
Re: Superdeterminism
Posted: Sun Dec 26, 2021 2:03 pm
by minkwe
Joy Christian wrote: ↑Sun Dec 26, 2021 1:43 pm
minkwe wrote: ↑Sun Dec 26, 2021 1:28 pm
Joy Christian wrote: ↑Sun Dec 26, 2021 12:33 pm
If a happens to be orthogonal to h (the measure of that happening, by the way, is nearly zero), then sign(h.a) is assumed to be equal to the sign of the first nonzero component from the set {a_x, a_y, a_z}. Bell does not specify this in his 1964 paper, but he does so in a later paper, and so do GHSZ in their paper.
.
Bell's function is A(a, h) = sign(a.h). What you describe above is a different function. I'm not sure this function containing "the sign of the first nonzero component from the set {a_x, a_y, a_z}" still makes perfect mathematical and physical sense?
(the measure of that happening, by the way, is nearly zero)
Nearly zero is not the same as zero.
The probability of h.a = 0 occurring in any real experiment is zero. But the special prescription I specified above for the case h.a = 0 eliminates that accidental possibility and makes sure that all results A = sign(h.a) are always nonzero. There are no zero or discarded results. No detection loophole.
I remain unconvinced that assuming setting dependent probability distribution of hidden variables makes physical sense. We are not doing mathematics.
.
Are you convinced that for the function I gave, p(h) =/= p(h|a) =/= p(h|ab)? Irrespective of whether you think the function makes physical sense.
Results that do not exist can not be called "discarded". This type of terminology is one of the antics used by Bell proponents. There are no zero, or "discarded" results in A(a,h) = -1/sign(a.h) either. In any real experiment, the probability of a = b is also zero. yet we use A(a, h) -= B(a, h) in the analysis to derive the inequality.
Re: Superdeterminism
Posted: Sun Dec 26, 2021 2:39 pm
by Joy Christian
minkwe wrote: ↑Sun Dec 26, 2021 2:03 pm
Joy Christian wrote: ↑Sun Dec 26, 2021 1:43 pm
minkwe wrote: ↑Sun Dec 26, 2021 1:28 pm
Bell's function is A(a, h) = sign(a.h). What you describe above is a different function. I'm not sure this function containing "the sign of the first nonzero component from the set {a_x, a_y, a_z}" still makes perfect mathematical and physical sense?
Nearly zero is not the same as zero.
The probability of h.a = 0 occurring in any real experiment is zero. But the special prescription I specified above for the case h.a = 0 eliminates that accidental possibility and makes sure that all results A = sign(h.a) are always nonzero. There are no zero or discarded results. No detection loophole.
I remain unconvinced that assuming setting dependent probability distribution of hidden variables makes physical sense. We are not doing mathematics.
.
Are you convinced that for the function I gave, p(h) =/= p(h|a) =/= p(h|ab)? Irrespective of whether you think the function makes physical sense.
Results that do not exist can not be called "discarded". This type of terminology is one of the antics used by Bell proponents. There are no zero, or "discarded" results in A(a,h) = -1/sign(a.h) either. In any real experiment, the probability of a = b is also zero. yet we use A(a, h) -= B(a, h) in the analysis to derive the inequality.
I am not convinced that assuming p(h|a, b) =/= p(h) models the physical experiments (or, more precisely, physical phenomena) accurately.
.
Re: Superdeterminism
Posted: Sun Dec 26, 2021 5:12 pm
by FrediFizzx
minkwe wrote: ↑Sun Dec 26, 2021 1:59 pm
FrediFizzx wrote: ↑Sun Dec 26, 2021 1:37 pm
minkwe wrote: ↑Sun Dec 26, 2021 1:11 pm
It is a vector for the function I provided. I'm allowed to define "h" that way according to Bell.
You didn't answer my question. What if "h" is a scalar?
.
then 1/sign(a.h) makes no sense since the dot product is meaningless for a scalar. Not sure what you are getting at though. The function I gave is for vectors, just like the one Bell gave also. I could envision another trivial case where both "a" and "h" are scalars, and A(a,h) -B(a, h) = -1/sign(a-h). In this case, we have exactly the same thing.
If a scalar then your whole argument makes no sense. And..., I'm really still not sure what you are getting at. I'll say it again..., you need to explain it better.
.
Re: Superdeterminism
Posted: Sun Dec 26, 2021 6:14 pm
by FrediFizzx
FrediFizzx wrote: ↑Sun Dec 26, 2021 5:12 pm
minkwe wrote: ↑Sun Dec 26, 2021 1:59 pm
FrediFizzx wrote: ↑Sun Dec 26, 2021 1:37 pm
You didn't answer my question. What if "h" is a scalar?
.
then 1/sign(a.h) makes no sense since the dot product is meaningless for a scalar. Not sure what you are getting at though. The function I gave is for vectors, just like the one Bell gave also. I could envision another trivial case where both "a" and "h" are scalars, and A(a,h) -B(a, h) = -1/sign(a-h). In this case, we have exactly the same thing.
If a scalar then your whole argument makes no sense. And..., I'm really still not sure what you are getting at. I'll say it again..., you need to explain it better.
Well actually, if "h" is a scalar then it would be just normal multiplication and you would have something like this,
Code: Select all
In[232]:= h = 0.5;
a
1/Sign[a*h]
Out[233]= {-0.144291, -0.525652, 0.838374}
Out[234]= {-1, -1, 1}
Which might mean something but don't know what.

.
Re: Superdeterminism
Posted: Sun Dec 26, 2021 11:44 pm
by gill1109
minkwe wrote: ↑Sun Dec 26, 2021 8:13 am
I don't think you guys are understanding me. I suspect that Richard understands but
as usual he wants to play games because
I've explained this to him before and he started scrambling to find a disingenuous way out.
Michel, whenever I say something which you don't want to believe, you start saying things like that. You keep making an assumption of bad faith on my part. Indeed, you've explained to me before and I've disagreed with your explanation before. I've explained why. So you now make an ad hominem attack on me. It looks to me as though you didn't understand my reasoning but you were scared it might convince other people, so you accuse me of playing games.
I think I did understand you perfectly well, and I think you are wrong. I tried to explain why. I think that Fred and Joy also both understood you perfectly well and also did not agree with you. For very good reasons.
Re: Superdeterminism
Posted: Mon Dec 27, 2021 12:35 am
by gill1109
Joy Christian wrote: ↑Sun Dec 26, 2021 12:33 pm
minkwe wrote: ↑Sun Dec 26, 2021 12:22 pm
Joy Christian wrote: ↑Sun Dec 26, 2021 12:07 pm
Bell's eq. (4) makes perfect mathematical and physical sense. The sign function simply picks out a normalized component of the spin vector, his lambda in eq. (4), about the detector vector
a, representing a scalar point +/-1 on a unit 2-sphere. That is analogous to what happens in a Stern–Gerlach apparatus.
Then you should not be surprised what A(a,h) = 1/sign(a.h) means physically. But wait, what scalar point does Bell's equation (4) give when those two vectors ("a", "h") are orthogonal?
If a happens to be orthogonal to h (the measure of that happening, by the way, is nearly zero), then sign(h.a) is assumed to be equal to the sign of the first nonzero component from the set {a_x, a_y, a_z}. Bell does not specify this in his 1964 paper, but he does so in a later paper, and so do GHSZ in their paper.
Nearly zero? Exactly zero, I think. For this reason, it does not matter how you define Bell's (4) when "a" and "h" are orthogonal. You could define it to always to equal +1 in that case. Or introduce a further hidden variable which is an independent fair coin toss [which actually never gets used!]. As Bell wrote "as the probability of this is zero we will not make special prescriptions for it". He doesn't bother to write down a special prescription because *any special prescription would do". He doesn't say that we should *discard outcomes from his mathematical model*.
There is simply no point in giving further details.
,
and
be vectors. Forget for a moment what those vectors mean physically. Focus on the maths.
, what is the domain of
, what is the domain of
)