Sci.Physics.Foundations

This isn't surprising. The function Sin[x]/x is called the Sinc function. It's defined in Mathematica, and Mathematica knows that the limit is 1.

jreed wrote: ↑Wed Mar 30, 2022 9:36 am This isn't surprising. The function Sin[x]/x is called the Sinc function. It's defined in Mathematica, and Mathematica knows that the limit is 1.

??? Wasn't meant to be surprising. Simply responding to Gill's question.
.

FrediFizzx wrote: ↑Tue Mar 29, 2022 3:23 am

gill1109 wrote: ↑Mon Mar 28, 2022 10:57 pm ...
Interesting. What do Mathematica and MathCad have to say about "lim_{x to 0} sin(x) / x"?

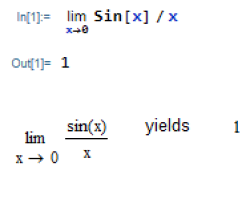
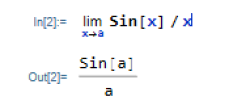
That is just the cursor bar at the end of that last x.
.

OK. Now substitute a = 0. You get 0/0.

I'm trying to get across to Fred that taking a limit by mere substitution does not always give the right answer.

Fred doesn't know the mathematical (epsilon-delta) definition of limit. Mathematica knows lots of things, but it manipulates symbols. The definition of limit depends on the topologies of the spaces you are working with. If you are not careful it will do formula manipulations which might be correct in the discrete topology but not correct in the usual topology of the real numbers.

gill1109 wrote: ↑Wed Apr 06, 2022 11:41 pm

FrediFizzx wrote: ↑Tue Mar 29, 2022 3:23 am

gill1109 wrote: ↑Mon Mar 28, 2022 10:57 pm ...
Interesting. What do Mathematica and MathCad have to say about "lim_{x to 0} sin(x) / x"?

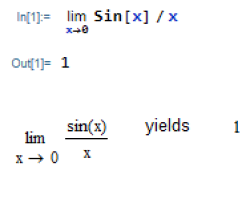
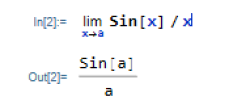
That is just the cursor bar at the end of that last x.
.

OK. Now substitute a = 0. You get 0/0.

I'm trying to get across to Fred that taking a limit by mere substitution does not always give the right answer.

Fred doesn't know the mathematical (epsilon-delta) definition of limit. Mathematica knows lots of things, but it manipulates symbols. The definition of limit depends on the topologies of the spaces you are working with. If you are not careful it will do formula manipulations which might be correct in the discrete topology but not correct in the usual topology of the real numbers.

Richard D. Gill, don't patronize Fred. Fred knows very well what "the mathematical (epsilon-delta) definition of limit" is. Unlike you Richard D. Gill, Fred has gone through the calculus course in high school. You, on the other hand, wrongly call yourself a "mathematician", which you are not. In fact, it is quite clear that you have never passed the first course in calculus. Moreover, you are prone to making extremely elementary mathematical mistakes, as I have repeatedly pointed out many times over the past ten years, for example in this paper: https://www.academia.edu/38423874/Refut ... ls_Theorem

Fred caught you out about making a bogus claim about the simple substitution rule for limits, the first rule one learns in calculus 101. So now you are trying to swindle nonsense about a completely different function that requires L' Hospital's rule before taking a limit. But even in that case "the mathematical (epsilon-delta) definition of limit" is not necessary, regardless of "the topologies of the spaces" one is working with, unless, like you, one has not passed a basic course in calculus and trying to swindle some nonsense because they have been caught out making yet another elementary mathematical mistake.

Mathematica knows how to take an x --> 0 limit even when an indeterminate function such as sin(x)/x is involved, as Fred clearly demonstrated. But more importantly, in Fred's calculations in his paper, no such indeterminate functions involving 0/0 or infinity/infinity are involved. No such indeterminate functions are involved in my work on Bell's dead theorem of the past fifteen years either. To bring them up in this context is therefore nothing but your usual strategy of deceiving the physics community by making a lot of noise about something completely irrelevant so that their attention is distracted from what has been achieved in the original work.

More importantly, Bell's theorem has been dead for the past fifteen years and you are a pathetic loser. You have wasted your life defending nonsense.
.

gill1109 wrote: ↑Wed Apr 06, 2022 11:41 pm

FrediFizzx wrote: ↑Tue Mar 29, 2022 3:23 am

gill1109 wrote: ↑Mon Mar 28, 2022 10:57 pm ...
Interesting. What do Mathematica and MathCad have to say about "lim_{x to 0} sin(x) / x"?

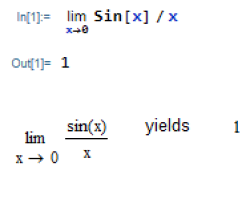
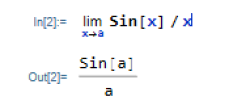
That is just the cursor bar at the end of that last x.
.

OK. Now substitute a = 0. You get 0/0.

Nope, unless you are looking for nonsense. Take the limit as a --> 0. I would have deleted your really stupid post if Joy hadn't responded to it. I think we have seen quite enough of your stupidity about this issue. Yep, we did limits in high school advanced math class and 3 semesters of calculus in college. Plus both Mathematica and MathCad know how to do calculus.
.

Simulation now published in the Mathematica Notebook Archive.

https://notebookarchive.org/local-quant ... 4-1eu4roy/
.

The new reverse order scenario works for the local QM prediction simulation also.





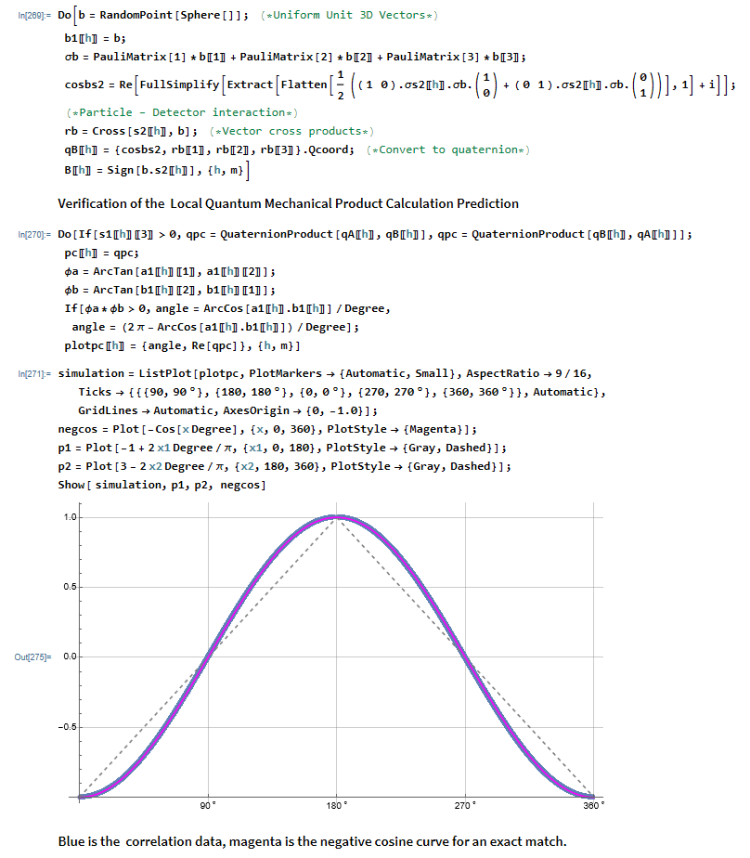
Still no hidden variable! Yep, Bell's junk physics theory is definitely a bunch of junk. It only takes 3-sphere topology to shoot down the Bell fanatics!
.

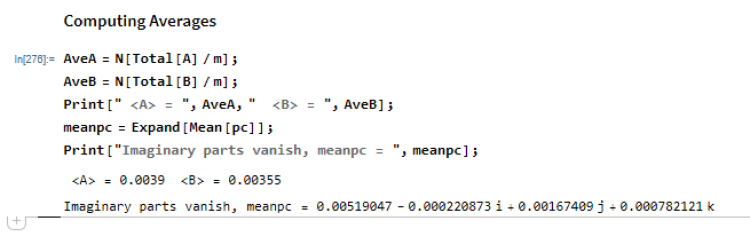
Here is the same thing but using the Quaternion Package that is built into Mathematica. It is faster than using the Clifford package. Note that I got rid of the silly "Qcoordinates" thing John Reed had devised. Conversion to quaternions is done more correctly now.





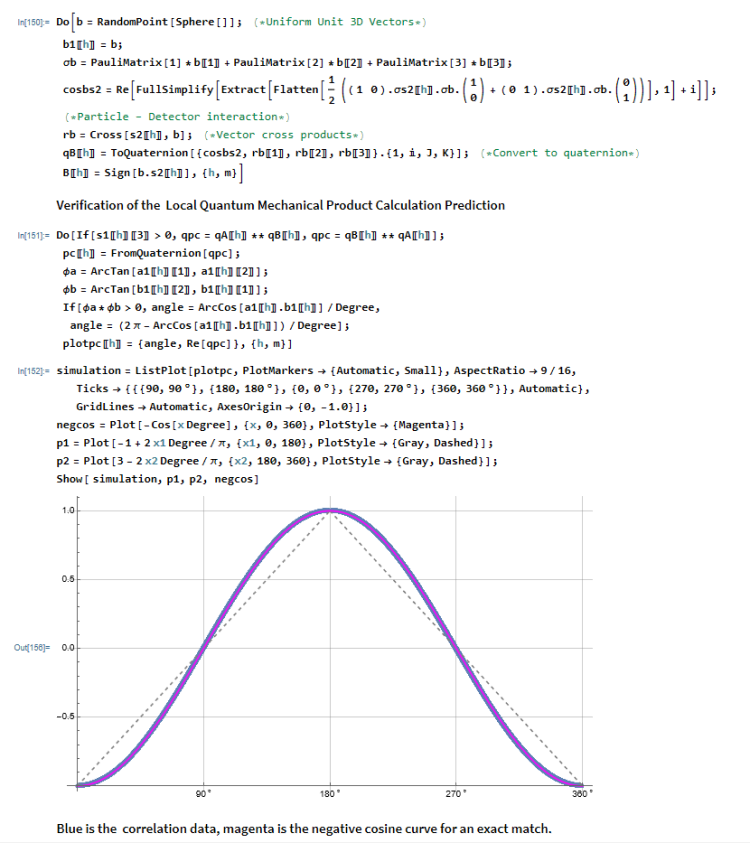
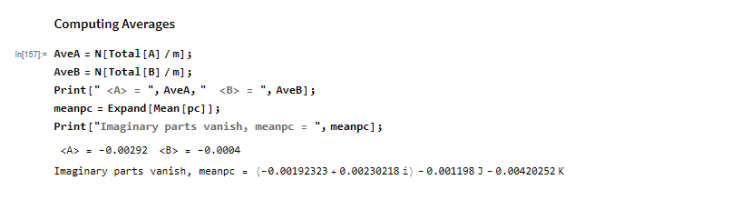
Enjoy another version that kills Bell's junk physics theory!
.

Here is the original version simplified a bit. The s_z component is not needed to zero out the imaginary cross product components. Nor is geometric algebra. It is all about quaternion multiplication and when the limits are taken. I'm updating the paper on ResearchGate to match this validation of the local QM prediction. r_0 has been taken out but is still there in the product calculation.





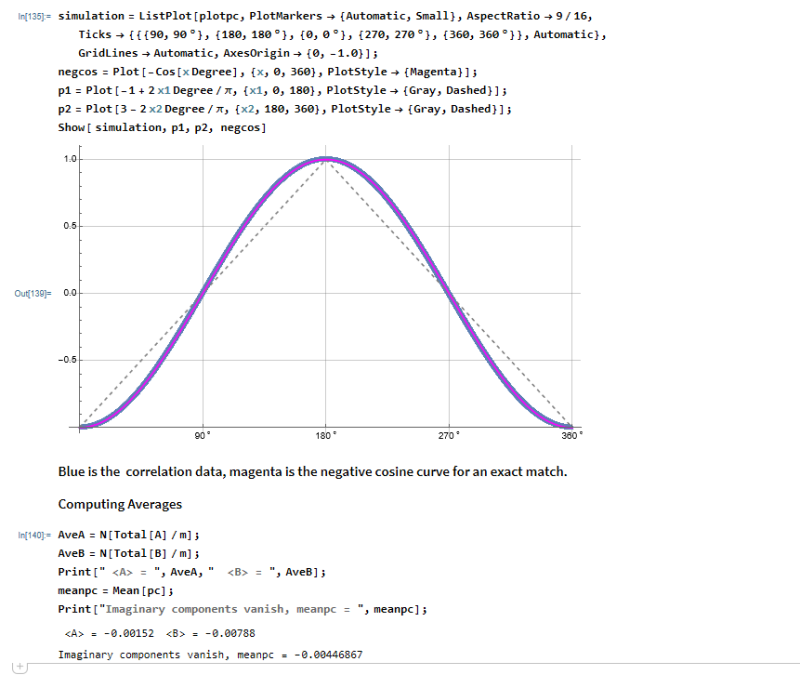
Enjoy another Bell killer!
.

I have decided to use the native quaternion package in Mathematica for the paper so here is the version for that.





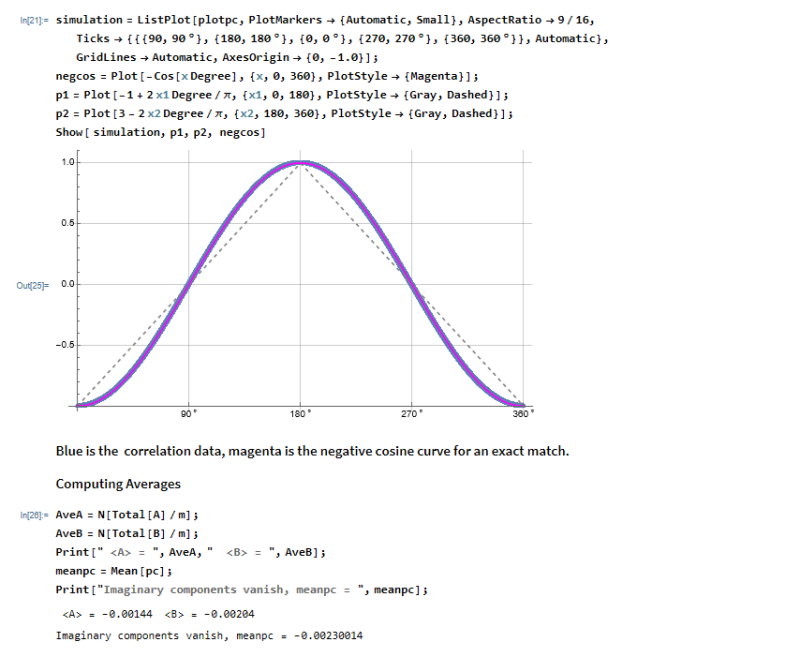
Here are the files,

sims/Local-QMprodcalc_archive4.pdf
sims/Local-QMprodcalc_archive4.nb

Enjoy another Bell killer!
.

I have revised the paper for this simulation.

http://dx.doi.org/10.13140/RG.2.2.22142.25927

Enjoy!
.

Thanks to Pierre Leroy, the above simulation has now been done in the C programming language.

http://pierrel5.free.fr/physique/loc_qm ... qm_FD.html

Enjoy!
.

I found a couple of mistakes in the previous simulation that didn't affect the results but have corrected them here.





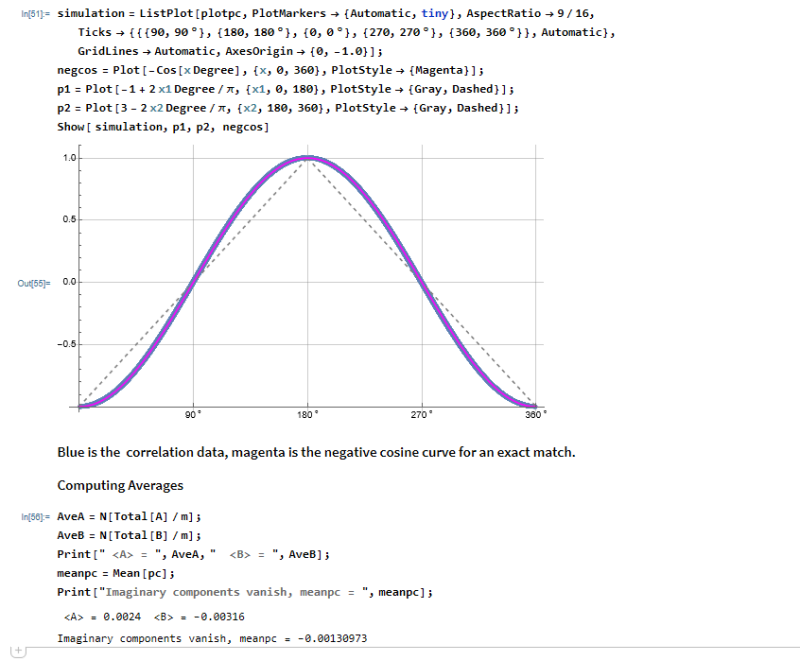
Typical qpc is now,
It's another Bell killer! Enjoy!
.