Superdeterminism

[FrediFizzx]

...
This is what is measured experimentally when we measure E(a,b).

No it is NOT! It is equal to zero and they don't get zero in the experiments. Use a better equation or stop talking about it.
.

[minkwe]

...
This is what is measured experimentally when we measure E(a,b).

No it is NOT! It is equal to zero and they don't get zero in the experiments. Use a better equation or stop talking about it.
.

Then I don't know what you are talking about. I don't see how you get zero. Even if you reduce it to



It is not necessarily zero. You only get zero if you assume that P(+1) = P(-1) = 0.5. But this is not necessarily the case.

[FrediFizzx]

...
This is what is measured experimentally when we measure E(a,b).

No it is NOT! It is equal to zero and they don't get zero in the experiments. Use a better equation or stop talking about it.
.

Then I don't know what you are talking about. I don't see how you get zero. Even if you reduce it to



It is not necessarily zero. You only get zero if you assume that P(+1) = P(-1) = 0.5. But this is not necessarily the case.

The vectors "c" and "d" have dropped out. The equation is nonsense. Please use a better equation. Thanks.
.

[gill1109]

No it is NOT! It is equal to zero and they don't get zero in the experiments. Use a better equation or stop talking about it.

Then I don't know what you are talking about. I don't see how you get zero. Even if you reduce it to

it is not necessarily zero. You only get zero if you assume that P(+1) = P(-1) = 0.5. But this is not necessarily the case.

The vectors "c" and "d" have dropped out. The equation is nonsense. Please use a better equation. Thanks.

Fred is right! His maths is better than Michel's in my opinion - for what it's worth (I'm just a statistician). Michel is better, in my opinion, at programming.

Hope everyone is enjoying a Christmas break! Best wishes for the New Year!

[Joy Christian]

In a typical EPRB experiment, you have a distribution produced by a source, and from that, you select a subset that produced the outcomes you observed when the settings were (a,b). p(h|a, b) =/= p(h) (also known as "superdeterminism") simply means that this subset is not the same as the source distribution.

If this is the claim of "superdeterminism", then it is completely false. There is never any selection of a subset of p(h) when experiments are done with a fixed set (a, b) of settings. ALL of the hidden variables h in H play role in the experiment, without exception. The assumption p(h|a, b) =/= p(h) is false.

The assumption p(h|a, b) =/= p(h) can hold if and only if the hidden variables h influence the spontaneous choices of the random settings a and b.
.

[gill1109]

In a typical EPRB experiment, you have a distribution produced by a source, and from that, you select a subset that produced the outcomes you observed when the settings were (a,b). p(h|a, b) =/= p(h) (also known as "superdeterminism") simply means that this subset is not the same as the source distribution.

If this is the claim of "superdeterminism", then it is completely false. There is never any selection of a subset of p(h) when experiments are done with a fixed set (a, b) of settings. ALL of the hidden variables h in H play role in the experiment, without exception. The assumption p(h|a, b) =/= p(h) is false.

The assumption p(h|a, b) =/= p(h) can hold if and only if the hidden variables h influence the spontaneous choices of the random settings a and b.
.

p(h|a, b) =/= p(h) is not an *assumption* of superdeterminism, it's a *consequence* of superdeterminism. According to superdeterminism, the very notion of a spontaneous choice is misguided. No spontaneous choices exist. Not even in our brains, which are also subject to the laws of physics. Which are deterministic laws. Differential equations, according to Tim Palmer (of Jesus College / Oxford University, BTW) and his friends.

I think it is an interesting mathematical-physical model which might be adequate for cosmology but which I think breaks down at the level of real life, including real life Bell-type experiments.

[Joy Christian]

In a typical EPRB experiment, you have a distribution produced by a source, and from that, you select a subset that produced the outcomes you observed when the settings were (a,b). p(h|a, b) =/= p(h) (also known as "superdeterminism") simply means that this subset is not the same as the source distribution.

If this is the claim of "superdeterminism", then it is completely false. There is never any selection of a subset of p(h) when experiments are done with a fixed set (a, b) of settings. ALL of the hidden variables h in H play role in the experiment, without exception. The assumption p(h|a, b) =/= p(h) is false.

The assumption p(h|a, b) =/= p(h) can hold if and only if the hidden variables h influence the spontaneous choices of the random settings a and b.
.

p(h|a, b) =/= p(h) is not an *assumption* of superdeterminism, it's a *consequence* of superdeterminism. According to superdeterminism, the very notion of a spontaneous choice is misguided. No spontaneous choices exist. Not even in our brains, which are also subject to the laws of physics. Which are deterministic laws. Differential equations, according to Tim Palmer (of Jesus College / Oxford University, BTW) and his friends.

I think it is an interesting mathematical-physical model which might be adequate for cosmology but which I think breaks down at the level of real life, including real life Bell-type experiments.

Tim and I have known each other for 30 years. Michel wants to deny any metaphysical assumption behind the claim p(h|a, b) =/= p(h). He wants to claim that a selection of the subset p(h|a, b) =/= p(h) is necessitated by the very act of choosing (a, b). But that is pure baloney.
.

[minkwe]

Fred is right!

Can someone please explain to me why Bell's equation 2 is equal to zero. What am I missing?

[FrediFizzx]

Fred is right!

Can someone please explain to me why Bell's equation 2 is equal to zero. What am I missing?

It is mainly because Bell didn't specify any actual functions for A and B other than equal to +/-1.
.

[minkwe]

Michel wants to deny any metaphysical assumption behind the claim p(h|a, b) =/= p(h).

I can't really engage with a misrepresentation of my position which I've explained multiple times.

p(h|a, b) =/= p(h) has absolutely no metaphysical "assumption" behind it. It's simply a statement that two distribution are different.

It is Bell who called this inequality "super-determinism". You should Investigate the origin of the term in the context of Bell's theorem. You (and Richard) are stuck with popular science representations of what "super-determinism" means. Not what it actually means. You've picked an absurd, nonsensical *reason* often provided in an attempt explain *why* p(h|a, b) =/= p(h). And you are unwilling to entertain the fact that such popular science claims are themselves absolutely distinct from the claim that. p(h|a, b) =/= p(h). The correct term for this phenomenon is "strawman".

If you want to believe that p(h|a, b) =/= p(h) must mean that the hidden variables determine the settings, as Gill says, or that it must mean the settings go back in time to determine the what the source produces, then I can't help you guys. Correlation is not causation. https://bayes.wustl.edu/etj/articles/cmystery.pdf, Pg 9-16

ALL of the hidden variables h in H play role in the experiment, without exception. The assumption p(h|a, b) =/= p(h) is false.

This is just a proclamation. What is the physical justification of it. I've asked many times but you have provided none.

I'm done. Happy new year guys!

[minkwe]

Fred is right!

Can someone please explain to me why Bell's equation 2 is equal to zero. What am I missing?

It is mainly because Bell didn't specify any actual functions for A and B other than equal to +/-1.
.

Fred, if this is what you and Richard are talking about, then you are very wrong. A(a,h) is a function producing either +1 or -1 depending on what values, a and h take . They are not constants.

Bell in fact gave candidate functions of this type in equation (4)

A(a,h) = - B(a,h) = -sign(a.h)

[FrediFizzx]

Michel wants to deny any metaphysical assumption behind the claim p(h|a, b) =/= p(h).

I can't really engage with a misrepresentation of my position which I've explained multiple times.

p(h|a, b) =/= p(h) has absolutely no metaphysical "assumption" behind it. It's simply a statement that two distribution are different.

It is Bell who called this inequality "super-determinism". You should Investigate the origin of the term in the context of Bell's theorem. You (and Richard) are stuck with popular science representations of what "super-determinism" means. Not what it actually means. You've picked an absurd, nonsensical *reason* often provided in an attempt explain *why* p(h|a, b) =/= p(h). And you are unwilling to entertain the fact that such popular science claims are themselves absolutely distinct from the claim that. p(h|a, b) =/= p(h). The correct term for this phenomenon is "strawman".

If you want to believe that p(h|a, b) =/= p(h) must mean that the hidden variables determine the settings, as Gill says, or that it must mean the settings go back in time to determine the what the source produces, then I can't help you guys. Correlation is not causation. https://bayes.wustl.edu/etj/articles/cmystery.pdf

ALL of the hidden variables h in H play role in the experiment, without exception. The assumption p(h|a, b) =/= p(h) is false.

This is just a proclamation. What is the physical justification of it. I've asked many times but you have provided none.

I'm done. Happy new year guys!

And..., I have already told you that "a" and "b" don't even exist when p(h) is created.

Happy New Year to you also and to everyone!
.

[FrediFizzx]

Can someone please explain to me why Bell's equation 2 is equal to zero. What am I missing?

It is mainly because Bell didn't specify any actual functions for A and B other than equal to +/-1.
.

Fred, if this is what you and Richard are talking about, then you are very wrong. A(a,h) is a function producing either +1 or -1 depending on what values, a and h take . They are not constants.

Bell in fact gave candidate functions of this type in equation (4)

A(a,h) = - B(a,h) = -sign(a.h)

Except we already know that is wrong so the function is rejected leaving only A = +/-1 and B = +/-1.
.

[FrediFizzx]

It is mainly because Bell didn't specify any actual functions for A and B other than equal to +/-1.
.

Fred, if this is what you and Richard are talking about, then you are very wrong. A(a,h) is a function producing either +1 or -1 depending on what values, a and h take . They are not constants.

Bell in fact gave candidate functions of this type in equation (4)

A(a,h) = - B(a,h) = -sign(a.h)

Except we already know that is wrong so the function is rejected leaving only A = +/-1 and B = +/-1.

Here are Joy's new functions that actually work.


.

[minkwe]

Fred are you saying, your functions above do not satisfy Bell's equation (1) of. A(a,h) = -B(a,h) = +/-1?

If not, then what makes you think they have any relationship to Bell's theorem? If they do, then Bell's equation (2) follows also. I don't understand how you can claim Bell's equation (2) is zero, but not for your functions. Your functions are just different ways of producing +/-1 depending on the settings and hidden variables ... I think.

[Joy Christian]

Michel wants to deny any metaphysical assumption behind the claim p(h|a, b) =/= p(h).

I can't really engage with a misrepresentation of my position which I've explained multiple times.

p(h|a, b) =/= p(h) has absolutely no metaphysical "assumption" behind it. It's simply a statement that two distribution are different.

It is Bell who called this inequality "super-determinism". You should Investigate the origin of the term in the context of Bell's theorem. You (and Richard) are stuck with popular science representations of what "super-determinism" means. Not what it actually means. You've picked an absurd, nonsensical *reason* often provided in an attempt explain *why* p(h|a, b) =/= p(h). And you are unwilling to entertain the fact that such popular science claims are themselves absolutely distinct from the claim that. p(h|a, b) =/= p(h). The correct term for this phenomenon is "strawman".

If you want to believe that p(h|a, b) =/= p(h) must mean that the hidden variables determine the settings, as Gill says, or that it must mean the settings go back in time to determine the what the source produces, then I can't help you guys. Correlation is not causation. https://bayes.wustl.edu/etj/articles/cmystery.pdf, Pg 9-16

ALL of the hidden variables h in H play role in the experiment, without exception. The assumption p(h|a, b) =/= p(h) is false.

This is just a proclamation. What is the physical justification of it. I've asked many times but you have provided none.

I'm done. Happy new year guys!

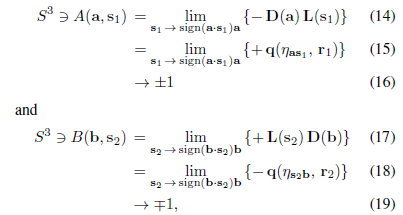
The assumption p(h|a, b) =/= p(h) is false without any metaphysical claims supporting it. The correct probability distribution is p(h), period. If
anyone wants to assume a new distribution p(h|a, b) =/= p(h) for every choice of spontaneously chosen settings (a, b), then they must justify it.
.

[FrediFizzx]

Fred are you saying, your functions above do not satisfy Bell's equation (1) of. A(a,h) = -B(a,h) = +/-1?

If not, then what makes you think they have any relationship to Bell's theorem? If they do, then Bell's equation (2) follows also. I don't understand how you can claim Bell's equation (2) is zero, but not for your functions. Your functions are just different ways of producing +/-1 depending on the settings and hidden variables ... I think.

Joy's functions do satisfy Bell's eq.(1) and don't end up being zero in the product calculation. If all you have is +/-1 to put into Bell's eq.(2) then you end up with zero for the complete product calculation. It's nonsense. And..., it is partially the reason Bell ended up with a junk physics theory instead of a real theorem.

Reference:
https://journals.aps.org/ppf/pdf/10.110 ... zika.1.195
.

[Joy Christian]

.

.

[gill1109]

If this is the claim of "superdeterminism", then it is completely false. There is never any selection of a subset of p(h) when experiments are done with a fixed set (a, b) of settings. ALL of the hidden variables h in H play role in the experiment, without exception. The assumption p(h|a, b) =/= p(h) is false.
The assumption p(h|a, b) =/= p(h) can hold if and only if the hidden variables h influence the spontaneous choices of the random settings a and b.

p(h|a, b) =/= p(h) is not an *assumption* of superdeterminism, it's a *consequence* of superdeterminism. According to superdeterminism, the very notion of a spontaneous choice is misguided. No spontaneous choices exist. Not even in our brains, which are also subject to the laws of physics. Which are deterministic laws. Differential equations, according to Tim Palmer (of Jesus College / Oxford University, BTW) and his friends.
I think it is an interesting mathematical-physical model which might be adequate for cosmology but which I think breaks down at the level of real life, including real life Bell-type experiments.

Tim and I have known each other for 30 years. Michel wants to deny any metaphysical assumption behind the claim p(h|a, b) =/= p(h). He wants to claim that a selection of the subset p(h|a, b) =/= p(h) is necessitated by the very act of choosing (a, b). But that is pure baloney.

I largely agree with you, Joy (and with Fred). Though I wouldn't talk about selection of a subset. Tim and his friends Sabine and Jonte are talking about inequality of probability distributions.

We need to distinguish between values which might be taken by random variables, random variables themselves, and the sets in which those random variables must take values. I would use three different letter-types for these three different things. For instance: a possible setting of Alice is denoted by plain lower case a, Alice's setting considered as a random variable is denoted by A, and the set of all possible values of Alice's setting is A. When Tim, Sabine, and Jonte write "p(h|a, b) =/= p(h)" they are talking about the inequality of conditional and unconditional probability distributions. They really mean that for (a, b) in a subset of AxB of positive probability, in those experiments in which the pair of settings (A, B) happens to take on a value in that subset, the probability distribution of H on H is not the same as what it is overall.

Not surprisingly, they prefer to use a common lazy physicist's or lazy statistician's notation. If you are not used to it you might be puzzled. If you see what they really mean you might still be puzzled. You have to get used to it. Probability 101.

Now, how could this be? It is a general principle that there is no correlation without causation. But the causation may be in one direction or the other, or from the past, or from the future. If there is correlation between (A, B) and H, then either (A, B) causes H, or H causes (A, B), or there is a common cause Z of both (A, B) and of H, or there is a common consequence Z of (A, B) and H and we are *selecting* cases on the basis of outcomes of Z.

Tim Palmer and his friends do argue that there is a common cause of *everything* hence all correlations which we see in the physical world are in some sense "spurious correlations". According to them, the correlations between settings and measurement outcomes in a Bell experiment is explained by "super hidden variables" which determine both the settings and the measurement outcomes and the hidden variables which physicists talk about. Super hidden variables behind the plain hidden variables.

I see that Joy and Fred more or less got the message but Michel is missing it.

Super-determinism can explain everything. But because it can explain everything, it really explains nothing. It is a religion, not a scientific hypothesis. No experiment can disprove it. It does not make any predictions.

[FrediFizzx]

Causation from the future is pure nonsense.
.