Re: Superdeterminism
Posted: Mon Dec 27, 2021 4:42 pm
Foundations of physics and/or philosophy of physics, and in particular, posts on unresolved or controversial issues
https://sciphysicsfoundations.com/
Then I don't know what you are talking about. I don't see how you get zero. Even if you reduce it toFrediFizzx wrote: ↑Mon Dec 27, 2021 4:42 pmNo it is NOT! It is equal to zero and they don't get zero in the experiments. Use a better equation or stop talking about it.
.
The vectors "c" and "d" have dropped out. The equation is nonsense. Please use a better equation. Thanks.minkwe wrote: ↑Mon Dec 27, 2021 4:46 pmThen I don't know what you are talking about. I don't see how you get zero. Even if you reduce it toFrediFizzx wrote: ↑Mon Dec 27, 2021 4:42 pmNo it is NOT! It is equal to zero and they don't get zero in the experiments. Use a better equation or stop talking about it.
.
It is not necessarily zero. You only get zero if you assume that P(+1) = P(-1) = 0.5. But this is not necessarily the case.
Fred is right! His maths is better than Michel's in my opinion - for what it's worth (I'm just a statistician). Michel is better, in my opinion, at programming.FrediFizzx wrote: ↑Mon Dec 27, 2021 5:39 pmThe vectors "c" and "d" have dropped out. The equation is nonsense. Please use a better equation. Thanks.minkwe wrote: ↑Mon Dec 27, 2021 4:46 pmThen I don't know what you are talking about. I don't see how you get zero. Even if you reduce it toFrediFizzx wrote: ↑Mon Dec 27, 2021 4:42 pm No it is NOT! It is equal to zero and they don't get zero in the experiments. Use a better equation or stop talking about it.
it is not necessarily zero. You only get zero if you assume that P(+1) = P(-1) = 0.5. But this is not necessarily the case.
If this is the claim of "superdeterminism", then it is completely false. There is never any selection of a subset of p(h) when experiments are done with a fixed set (a, b) of settings. ALL of the hidden variables h in H play role in the experiment, without exception. The assumption p(h|a, b) =/= p(h) is false.minkwe wrote: ↑Mon Dec 27, 2021 1:52 pm In a typical EPRB experiment, you have a distribution produced by a source, and from that, you select a subset that produced the outcomes you observed when the settings were (a,b). p(h|a, b) =/= p(h) (also known as "superdeterminism") simply means that this subset is not the same as the source distribution.
p(h|a, b) =/= p(h) is not an *assumption* of superdeterminism, it's a *consequence* of superdeterminism. According to superdeterminism, the very notion of a spontaneous choice is misguided. No spontaneous choices exist. Not even in our brains, which are also subject to the laws of physics. Which are deterministic laws. Differential equations, according to Tim Palmer (of Jesus College / Oxford University, BTW) and his friends.Joy Christian wrote: ↑Tue Dec 28, 2021 12:14 amIf this is the claim of "superdeterminism", then it is completely false. There is never any selection of a subset of p(h) when experiments are done with a fixed set (a, b) of settings. ALL of the hidden variables h in H play role in the experiment, without exception. The assumption p(h|a, b) =/= p(h) is false.minkwe wrote: ↑Mon Dec 27, 2021 1:52 pm In a typical EPRB experiment, you have a distribution produced by a source, and from that, you select a subset that produced the outcomes you observed when the settings were (a,b). p(h|a, b) =/= p(h) (also known as "superdeterminism") simply means that this subset is not the same as the source distribution.
The assumption p(h|a, b) =/= p(h) can hold if and only if the hidden variables h influence the spontaneous choices of the random settings a and b.
.
Tim and I have known each other for 30 years. Michel wants to deny any metaphysical assumption behind the claim p(h|a, b) =/= p(h). He wants to claim that a selection of the subset p(h|a, b) =/= p(h) is necessitated by the very act of choosing (a, b). But that is pure baloney.gill1109 wrote: ↑Tue Dec 28, 2021 12:32 amp(h|a, b) =/= p(h) is not an *assumption* of superdeterminism, it's a *consequence* of superdeterminism. According to superdeterminism, the very notion of a spontaneous choice is misguided. No spontaneous choices exist. Not even in our brains, which are also subject to the laws of physics. Which are deterministic laws. Differential equations, according to Tim Palmer (of Jesus College / Oxford University, BTW) and his friends.Joy Christian wrote: ↑Tue Dec 28, 2021 12:14 amIf this is the claim of "superdeterminism", then it is completely false. There is never any selection of a subset of p(h) when experiments are done with a fixed set (a, b) of settings. ALL of the hidden variables h in H play role in the experiment, without exception. The assumption p(h|a, b) =/= p(h) is false.minkwe wrote: ↑Mon Dec 27, 2021 1:52 pm In a typical EPRB experiment, you have a distribution produced by a source, and from that, you select a subset that produced the outcomes you observed when the settings were (a,b). p(h|a, b) =/= p(h) (also known as "superdeterminism") simply means that this subset is not the same as the source distribution.
The assumption p(h|a, b) =/= p(h) can hold if and only if the hidden variables h influence the spontaneous choices of the random settings a and b.
.
I think it is an interesting mathematical-physical model which might be adequate for cosmology but which I think breaks down at the level of real life, including real life Bell-type experiments.
I can't really engage with a misrepresentation of my position which I've explained multiple times.Joy Christian wrote: ↑Tue Dec 28, 2021 12:44 am Michel wants to deny any metaphysical assumption behind the claim p(h|a, b) =/= p(h).
This is just a proclamation. What is the physical justification of it. I've asked many times but you have provided none.ALL of the hidden variables h in H play role in the experiment, without exception. The assumption p(h|a, b) =/= p(h) is false.
Fred, if this is what you and Richard are talking about, then you are very wrong. A(a,h) is a function producing either +1 or -1 depending on what values, a and h take . They are not constants.FrediFizzx wrote: ↑Tue Dec 28, 2021 3:41 amIt is mainly because Bell didn't specify any actual functions for A and B other than equal to +/-1.
.
And..., I have already told you that "a" and "b" don't even exist when p(h) is created.minkwe wrote: ↑Tue Dec 28, 2021 4:12 amI can't really engage with a misrepresentation of my position which I've explained multiple times.Joy Christian wrote: ↑Tue Dec 28, 2021 12:44 am Michel wants to deny any metaphysical assumption behind the claim p(h|a, b) =/= p(h).
p(h|a, b) =/= p(h) has absolutely no metaphysical "assumption" behind it. It's simply a statement that two distribution are different.
It is Bell who called this inequality "super-determinism". You should Investigate the origin of the term in the context of Bell's theorem. You (and Richard) are stuck with popular science representations of what "super-determinism" means. Not what it actually means. You've picked an absurd, nonsensical *reason* often provided in an attempt explain *why* p(h|a, b) =/= p(h). And you are unwilling to entertain the fact that such popular science claims are themselves absolutely distinct from the claim that. p(h|a, b) =/= p(h). The correct term for this phenomenon is "strawman".
If you want to believe that p(h|a, b) =/= p(h) must mean that the hidden variables determine the settings, as Gill says, or that it must mean the settings go back in time to determine the what the source produces, then I can't help you guys. Correlation is not causation. https://bayes.wustl.edu/etj/articles/cmystery.pdf
This is just a proclamation. What is the physical justification of it. I've asked many times but you have provided none.ALL of the hidden variables h in H play role in the experiment, without exception. The assumption p(h|a, b) =/= p(h) is false.
I'm done. Happy new year guys!
Except we already know that is wrong so the function is rejected leaving only A = +/-1 and B = +/-1.minkwe wrote: ↑Tue Dec 28, 2021 4:20 amFred, if this is what you and Richard are talking about, then you are very wrong. A(a,h) is a function producing either +1 or -1 depending on what values, a and h take . They are not constants.FrediFizzx wrote: ↑Tue Dec 28, 2021 3:41 amIt is mainly because Bell didn't specify any actual functions for A and B other than equal to +/-1.
.
Bell in fact gave candidate functions of this type in equation (4)
A(a,h) = - B(a,h) = -sign(a.h)
Here are Joy's new functions that actually work.FrediFizzx wrote: ↑Tue Dec 28, 2021 4:24 amExcept we already know that is wrong so the function is rejected leaving only A = +/-1 and B = +/-1.minkwe wrote: ↑Tue Dec 28, 2021 4:20 amFred, if this is what you and Richard are talking about, then you are very wrong. A(a,h) is a function producing either +1 or -1 depending on what values, a and h take . They are not constants.FrediFizzx wrote: ↑Tue Dec 28, 2021 3:41 am
It is mainly because Bell didn't specify any actual functions for A and B other than equal to +/-1.
.
Bell in fact gave candidate functions of this type in equation (4)
A(a,h) = - B(a,h) = -sign(a.h)
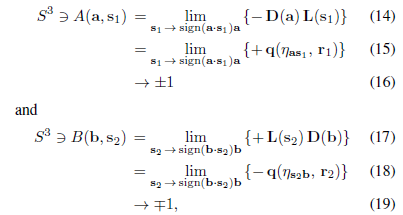
The assumption p(h|a, b) =/= p(h) is false without any metaphysical claims supporting it. The correct probability distribution is p(h), period. Ifminkwe wrote: ↑Tue Dec 28, 2021 4:12 amI can't really engage with a misrepresentation of my position which I've explained multiple times.Joy Christian wrote: ↑Tue Dec 28, 2021 12:44 am Michel wants to deny any metaphysical assumption behind the claim p(h|a, b) =/= p(h).
p(h|a, b) =/= p(h) has absolutely no metaphysical "assumption" behind it. It's simply a statement that two distribution are different.
It is Bell who called this inequality "super-determinism". You should Investigate the origin of the term in the context of Bell's theorem. You (and Richard) are stuck with popular science representations of what "super-determinism" means. Not what it actually means. You've picked an absurd, nonsensical *reason* often provided in an attempt explain *why* p(h|a, b) =/= p(h). And you are unwilling to entertain the fact that such popular science claims are themselves absolutely distinct from the claim that. p(h|a, b) =/= p(h). The correct term for this phenomenon is "strawman".
If you want to believe that p(h|a, b) =/= p(h) must mean that the hidden variables determine the settings, as Gill says, or that it must mean the settings go back in time to determine the what the source produces, then I can't help you guys. Correlation is not causation. https://bayes.wustl.edu/etj/articles/cmystery.pdf, Pg 9-16
This is just a proclamation. What is the physical justification of it. I've asked many times but you have provided none.ALL of the hidden variables h in H play role in the experiment, without exception. The assumption p(h|a, b) =/= p(h) is false.
I'm done. Happy new year guys!
Joy's functions do satisfy Bell's eq.(1) and don't end up being zero in the product calculation. If all you have is +/-1 to put into Bell's eq.(2) then you end up with zero for the complete product calculation. It's nonsense. And..., it is partially the reason Bell ended up with a junk physics theory instead of a real theorem.minkwe wrote: ↑Tue Dec 28, 2021 4:46 am Fred are you saying, your functions above do not satisfy Bell's equation (1) of. A(a,h) = -B(a,h) = +/-1?
If not, then what makes you think they have any relationship to Bell's theorem? If they do, then Bell's equation (2) follows also. I don't understand how you can claim Bell's equation (2) is zero, but not for your functions. Your functions are just different ways of producing +/-1 depending on the settings and hidden variables ... I think.

I largely agree with you, Joy (and with Fred). Though I wouldn't talk about selection of a subset. Tim and his friends Sabine and Jonte are talking about inequality of probability distributions.Joy Christian wrote: ↑Tue Dec 28, 2021 12:44 amTim and I have known each other for 30 years. Michel wants to deny any metaphysical assumption behind the claim p(h|a, b) =/= p(h). He wants to claim that a selection of the subset p(h|a, b) =/= p(h) is necessitated by the very act of choosing (a, b). But that is pure baloney.gill1109 wrote: ↑Tue Dec 28, 2021 12:32 amp(h|a, b) =/= p(h) is not an *assumption* of superdeterminism, it's a *consequence* of superdeterminism. According to superdeterminism, the very notion of a spontaneous choice is misguided. No spontaneous choices exist. Not even in our brains, which are also subject to the laws of physics. Which are deterministic laws. Differential equations, according to Tim Palmer (of Jesus College / Oxford University, BTW) and his friends.Joy Christian wrote: ↑Tue Dec 28, 2021 12:14 am If this is the claim of "superdeterminism", then it is completely false. There is never any selection of a subset of p(h) when experiments are done with a fixed set (a, b) of settings. ALL of the hidden variables h in H play role in the experiment, without exception. The assumption p(h|a, b) =/= p(h) is false.
The assumption p(h|a, b) =/= p(h) can hold if and only if the hidden variables h influence the spontaneous choices of the random settings a and b.
I think it is an interesting mathematical-physical model which might be adequate for cosmology but which I think breaks down at the level of real life, including real life Bell-type experiments.