Sci.Physics.Foundations

Posted: **Mon Nov 08, 2021 12:57 am**

This little theorem appears in many publications.

Let $X_1, X_2, Y_1, Y_2$ be four random variables taking the values +/-1
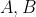
Let $A, B$ be two random variables taking the values 1, 2
Suppose (A, B) is statistically independent of $(X_1, X_2, Y_1, Y_2)$
Define $X = X_A$ and $Y = Y_B$
In other words, $X = X_1$ if $A =1$ , $X = X_2$ if $A = 2$ ; $Y = Y_1$ if $B = 1$ , $Y = Y_2$ if $B = 2$
Define $\rho_{ab} = E(XY | A = a, B = b)$

Theorem: $\rho_{11} - \rho_{12} - \rho_{21} - \rho_{22}$ lies between -2 and +2

Proof:

$X_1 Y_1 - X_1 Y_2 - X_2 Y_1 - X_2 Y_2 = X_1 (Y_1 - Y_2) - X_2 (Y_1 + Y_2)$ can only take the values +/-2

Hence
$E(X_1 Y_1) - E(X_1 Y_2) - E(X_2 Y_2) - E(X_2 Y_2)$ lies between -2 and +2

But $E(X_1 Y_1) = E(X_1 Y_1 | A = 1, B = 1)$ by statistical independence of $(X_1, X_2, Y_1, Y_2)$ from $(A, B)$
$= E(X Y | A=1, B =1)$ . because $X Y = X_1 Y_1$ when $A = 1, B = 1$
$= \rho_{11}$

In the same way, $\rho_{ab} = E(X_a Y_b)$ for all $a, b = 1,2$

QED

Posted: **Mon Nov 08, 2021 5:13 am**

@gill1109 What the heck is this? A proof of the CHSH inequality? That is NOT what I asked for.

Please demonstrate how QM or the experiments exceed the bounds on the CHSH inequality.
.

Posted: **Mon Nov 08, 2021 6:27 am**

FrediFizzx wrote: ↑Mon Nov 08, 2021 5:13 am @gill1109 What the heck is this? A proof of the CHSH inequality? That is NOT what I asked for.

Please demonstrate how QM or the experiments exceed the bounds on the CHSH inequality.

Fred, this is the maths part of the forum. I told you some mathematical facts. Do you agree with them?

On the physics side, we could discuss what relevance, if any, this maths result has for physics.

If you would set up a computer science section, I could discuss the relevance, if any, that this result has for distributed computing.

But anyway, since you asked: one can use conventional QM to compute that "S" could maximally equal to 2 sqrt 2. That's called the Tsirelson inequality. I hope you are familiar with it. Joy also derived that inequality, with his approach.

How do experiments exceed the bounds? Well, they collect data, and they calculate the obvious estimates of those four correlations, and they saw that they were bigger than 2. In Delft they observed about 2.4. In Munich about 2.6. In Vienna and at NIST about 2.0001.

But Delft and Munich had much too small "N" so maybe this was just chance. Vienna and NIST had "N" of the order of hundreds of millions. So their error bars are tiny. But one can still complain about some features of the data they collected.

How do computer simulations exceed the bounds? Obviously, by not satisfying the conditions under which the bounds are derived.

Posted: **Mon Nov 08, 2021 6:50 am**

gill1109 wrote: ↑Mon Nov 08, 2021 6:27 am
FrediFizzx wrote: ↑Mon Nov 08, 2021 5:13 am @gill1109 What the heck is this? A proof of the CHSH inequality? That is NOT what I asked for.

Please demonstrate how QM or the experiments exceed the bounds on the CHSH inequality.
... How do experiments exceed the bounds? Well, they collect data, and they calculate the obvious estimates of those four correlations, and they saw that they were bigger than 2. In Delft they observed about 2.4. In Munich about 2.6. In Vienna and at NIST about 2.0001. ...

Please demonstrate MATHEMATICALLY how QM or the experiments exceed the bounds on the CHSH inequality while using the CHSH inequality.
.

Posted: **Mon Nov 08, 2021 12:50 pm**

@gill1109 Yeah, didn't think you could do it since it is IMPOSSIBLE!
.

Posted: **Mon Nov 08, 2021 5:00 pm**

gill1109 wrote: ↑Mon Nov 08, 2021 12:57 am This little theorem appears in many publications.

Let $X_1, X_2, Y_1, Y_2$ be four random variables taking the values +/-1
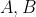
Let $A, B$ be two random variables taking the values 1, 2
Suppose (A, B) is statistically independent of $(X_1, X_2, Y_1, Y_2)$
Define $X = X_A$ and $Y = Y_B$
In other words, $X = X_1$ if $A =1$ , $X = X_2$ if $A = 2$ ; $Y = Y_1$ if $B = 1$ , $Y = Y_2$ if $B = 2$
Define $\rho_{ab} = E(XY | A = a, B = b)$

Theorem: $\rho_{11} - \rho_{12} - \rho_{21} - \rho_{22}$ lies between -2 and +2

Proof:

$X_1 Y_1 - X_1 Y_2 - X_2 Y_1 - X_2 Y_2 = X_1 (Y_1 - Y_2) - X_2 (Y_1 + Y_2)$ can only take the values +/-2

Hence
$E(X_1 Y_1) - E(X_1 Y_2) - E(X_2 Y_2) - E(X_2 Y_2)$ lies between -2 and +2

But $E(X_1 Y_1) = E(X_1 Y_1 | A = 1, B = 1)$ by statistical independence of $(X_1, X_2, Y_1, Y_2)$ from $(A, B)$
$= E(X Y | A=1, B =1)$ . because $X Y = X_1 Y_1$ when $A = 1, B = 1$
$= \rho_{11}$

In the same way, $\rho_{ab} = E(X_a Y_b)$ for all $a, b = 1,2$

QED

Richard, your theorem is superfluous. The bounds have nothing to do with probability theory. The first two statements are sufficient to derive the bounds. There is no need for any consideration of probability distributions, or any other physical notions. It is a tautology of mathematics. In fact, you are aware that I've shown this very theorem a long time ago. Here it is again, with all the nonsense removed:

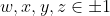
Given four numbers $w,x,y,z \in \pm 1$ the consider the expression

$wx - wz + yx + yz = w(x-z) + (x+z)$

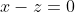
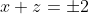
since they terms can only take values $\pm 1$ , it follows that when $x-z = 0$ is 0, then necessarily, $x+z = \pm 2$ and vice versa. Therefore, at extrema, one of the terms will be zero and the other will either be +2 or -2. Therefore
$wx - wz + yx + yz = w(x-z) + (x+z) \le 2$

Given any sequence of such four numbers, of any length N, it follows that:
$\left | \frac{1}{N} \sum_{i}^{N} w_ix_i - \frac{1}{N} \sum_{i}^{N} w_iz_i \right | + \left | \frac{1}{N} \sum_{i}^{N} y_ix_i + \frac{1}{N} \sum_{i}^{N} y_iz_i \right |$

$\le \frac{1}{N} \sum_{i}^{N} \left | w_i \right | \left |x_i - z_i \right | + \frac{1}{N} \sum_{i}^{N} \left | w_i \right | \left |x_i + z_i \right | = 2$

Therefore

$\left | \frac{1}{N} \sum_{i}^{N} w_ix_i - \frac{1}{N} \sum_{i}^{N} w_iz_i \right | + \left | \frac{1}{N} \sum_{i}^{N} y_ix_i + \frac{1}{N} \sum_{i}^{N} y_iz_i \right | \le 2$

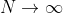
This upper bound applies to for any length of the spreadsheet but you can see easily that as $N \rightarrow \infty$ , we have

$\left \langle wx \right \rangle - \left \langle wz \right \rangle + \left \langle yx \right \rangle + \left \langle yz \right \rangle \le \left | \left \langle wx \right \rangle - \left \langle wz \right \rangle \right | + \left | \left \langle yx \right \rangle + \left \langle yz \right \rangle \right | \le 2$

There is no need to invoke any concept of locality, or realism to derive these limits and these limits.

Posted: **Mon Nov 08, 2021 6:54 pm**

minkwe wrote: ↑Mon Nov 08, 2021 5:00 pm Richard, your theorem is superfluous. The bounds have nothing to do with probability theory. The first two statements are sufficient to derive the bounds. There is no need for any consideration of probability distributions, or any other physical notions. It is a tautology of mathematics. In fact, you are aware that I've shown this very theorem a long time ago. Here it is again, with all the nonsense removed:

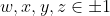
Given four numbers $w,x,y,z \in \pm 1$ the consider the expression

$wx - wz + yx + yz = w(x-z) + (x+z)$

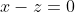
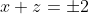
since they terms can only take values $\pm 1$ , it follows that when $x-z = 0$ is 0, then necessarily, $x+z = \pm 2$ and vice versa. Therefore, at extrema, one of the terms will be zero and the other will either be +2 or -2. Therefore
$wx - wz + yx + yz = w(x-z) + (x+z) \le 2$

Given any sequence of such four numbers, of any length N, it follows that:
$\left | \frac{1}{N} \sum_{i}^{N} w_ix_i - \frac{1}{N} \sum_{i}^{N} w_iz_i \right | + \left | \frac{1}{N} \sum_{i}^{N} y_ix_i + \frac{1}{N} \sum_{i}^{N} y_iz_i \right |$

$\le \frac{1}{N} \sum_{i}^{N} \left | w_i \right | \left |x_i - z_i \right | + \frac{1}{N} \sum_{i}^{N} \left | w_i \right | \left |x_i + z_i \right | = 2$

Therefore

$\left | \frac{1}{N} \sum_{i}^{N} w_ix_i - \frac{1}{N} \sum_{i}^{N} w_iz_i \right | + \left | \frac{1}{N} \sum_{i}^{N} y_ix_i + \frac{1}{N} \sum_{i}^{N} y_iz_i \right | \le 2$

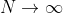
This upper bound applies to for any length of the spreadsheet but you can see easily that as $N \rightarrow \infty$ , we have

$\left \langle wx \right \rangle - \left \langle wz \right \rangle + \left \langle yx \right \rangle + \left \langle yz \right \rangle \le \left | \left \langle wx \right \rangle - \left \langle wz \right \rangle \right | + \left | \left \langle yx \right \rangle + \left \langle yz \right \rangle \right | \le 2$

There is no need to invoke any concept of locality, or realism to derive these limits and these limits.

Dear Michel,

Your proof does not prove my theorem. Actually, I don’t see that what you prove has much interest, whether to physics or to computer science, but in this part of the forum we talk about mathematics.

I wrote out a little theorem and its simple proof in elementary probability theory. Discrete random variables, probabilities and conditional probabilities, expectation value, conditional expectation.

I did not invoke any physical concepts at all.

I did not take any limits. I did not introduce any spreadsheets.

My theorem concerns the conditional expectations E(XY | A = a, B = b), you do not even mention them.

Would you like me to write out the standard elementary probability theory definition of E(XY | A = a, B = b)?

Would you like me to explain the relevance of my theorem in the mathematics of computer science - distributed computing?

Richard

Posted: **Mon Nov 08, 2021 7:12 pm**

Dear Fred,

You wrote:

Please demonstrate MATHEMATICALLY how QM or the experiments exceed the bounds on the CHSH inequality while using the CHSH inequality.

and then:

FrediFizzx wrote: ↑Mon Nov 08, 2021 12:50 pm @gill1109 Yeah, didn't think you could do it since it is IMPOSSIBLE!

I can’t do what you said because I don’t understand what you mean.

QM predicts violation of the Bell-CHSH inequality but doesn’t explain how it is done, unless you go for action at a distance (spooky collapse of the wave function).

The experiments violate the inequality by collecting data, an N x 4 spreadsheet with columns called A, B filled with 1’s and 2’s and columns called X, Y filled with +/-1’s. They then spit this into 4 subsets of rows corresponding to four values of (a, b). They then average x times y for each of the four subsets.

In principle, one of the four correlations minus the sum of the other three could equal -4 or +4 or many different values in between.

Your simulation violates the inequality just like real experiments do: by building such a spreadsheet as I just described.

Posted: **Mon Nov 08, 2021 11:13 pm**

@gill1109 What a bunch of nonsense. I should just delete your junk above.

Please demonstrate MATHEMATICALLY how QM or the experiments exceed the bounds on the CHSH inequality while using the CHSH inequality.
.

Posted: **Tue Nov 09, 2021 4:53 am**

gill1109 wrote: ↑Mon Nov 08, 2021 6:54 pm Actually, I don’t see that what you prove has much interest, whether to physics or to computer science, but in this part of the forum we talk about mathematics.

I wrote out a little theorem and its simple proof in elementary probability theory. Discrete random variables, probabilities and conditional probabilities, expectation value, conditional expectation.

At least you admit that Bell's inequalities have no interest to physics or computer science. My point was that the first two statements determine the limit and nothing else that you state about probability theory matters to obtain the derived limits. You can dress them up with "probability theory" but it's all the same proof. All the garbage is superfluous subterfuge.

gill1109 wrote: ↑Mon Nov 08, 2021 6:54 pm I did not invoke any physical concepts at all.
I did not take any limits. I did not introduce any spreadsheets.

FrediFizzx wrote: ↑Mon Nov 08, 2021 12:50 pm The experiments violate the inequality by collecting data, an N x 4 spreadsheet with columns called A, B filled with 1’s and 2’s and columns called X, Y filled with +/-1’s. They then spit this into 4 subsets of rows corresponding to four values of (a, b). They then average x times y for each of the four subsets.

gill1109 wrote: ↑Mon Nov 08, 2021 6:54 pm My theorem concerns the conditional expectations E(XY | A = a, B = b), you do not even mention them.

Would you like me to write out the standard elementary probability theory definition of E(XY | A = a, B = b)?

Would you like me to explain the relevance of my theorem in the mathematics of computer science - distributed computing?

Richard, you've been away from England so much you are starting to fail to understand basic English: Kansrekening is niet nodig. Therefore any discordance with the derived bounds points to an error in the application of the derived inequality. Nobody here denies the validity of Bell's inequalities. Perhaps one day you will stop barking at the moon about the validity of Bell's inequalities. You need a new game, the old one is boring.

Posted: **Tue Nov 09, 2021 7:48 am**

minkwe wrote: ↑Tue Nov 09, 2021 4:53 am At least you admit that Bell's inequalities have no interest to physics or computer science. My point was that the first two statements determine the limit and nothing else that you state about probability theory matters to obtain the derived limits. You can dress them up with "probability theory" but it's all the same proof. All the garbage is superfluous subterfuge.

gill1109 wrote: ↑Mon Nov 08, 2021 6:54 pm My theorem concerns the conditional expectations E(XY | A = a, B = b), you do not even mention them.
Would you like me to write out the standard elementary probability theory definition of E(XY | A = a, B = b)?
Would you like me to explain the relevance of my theorem in the mathematics of computer science - distributed computing?
Richard, you've been away from England so much you are starting to fail to understand basic English: Kansrekening is niet nodig. Therefore any discordance with the derived bounds points to an error in the application of the derived inequality. Nobody here denies the validity of Bell's inequalities. Perhaps one day you will stop barking at the moon about the validity of Bell's inequalities. You need a new game, the old one is boring.

Michel

We disagree on the question: what are Bell inequalities. You proved a different inequality from the one I proved.

I did not say that what I see as the mathematical core of Bell's work has no interest to physics or computer science.

You derived a different (and more easy) mathematical result, which I do think has no interest at all to physics or computer science.

I believe that my (more difficult) result has great interest to physics and to computer science! But I present it here as pure mathematics so that we might agree on its mathematical truth before debating whether or not it means anything in physics or to computer science. Two more, different debates. (0) what does it mean? (1) is it true? (2) relevance to computer science? (3) relevance to physics?

Yours
Richard

PS My "theorem" (along with its proof) has been published several times, to being with, about 20 years ago in PNAS and in Europhysics Letters, and more recently, last year in IEEE Access. Nobody has ever pointed out an error in those proofs. A generalisation of my theorem was published in several papers around 2001 and a further refinement (strengthening) in 2015 in Nature.

It seems that real physicists found it interesting and useful.

I write the word "theorem" in quotes because the proof is simple and it is just some simple probability theory. But I repeat: my theorem is not the same as your theorem! Mine is useful, yours is useless!

Posted: **Tue Nov 09, 2021 7:51 am**

@gill1109

Please demonstrate MATHEMATICALLY how QM or the experiments exceed the bounds on the CHSH inequality while using the CHSH inequality.
.

Posted: **Tue Nov 09, 2021 7:58 am**

FrediFizzx wrote: ↑Tue Nov 09, 2021 7:51 am @gill1109

Please demonstrate MATHEMATICALLY how QM or the experiments exceed the bounds on the CHSH inequality while using the CHSH inequality.

No. First of all, I want to establish agreement on the inequality which I derived. It is not what you think it is. It's a true mathematical result. It is not what you think of as the CHSH inequality.

By the way,

(1) I don't think anyone should "use" it in the way you seem to mean by that word

(2) I can't explain how QM violates it

(3) It is trivial to understand how data might violate it

(4) The conclusion of my theorem need not hold if its assumptions do not hold. That explains why your simulation, Fred, does violate the inequality.

Posted: **Tue Nov 09, 2021 8:58 am**

gill1109 wrote: ↑Tue Nov 09, 2021 7:58 am
FrediFizzx wrote: ↑Tue Nov 09, 2021 7:51 am @gill1109

Please demonstrate MATHEMATICALLY how QM or the experiments exceed the bounds on the CHSH inequality while using the CHSH inequality.
No. First of all, I want to establish agreement on the inequality which I derived. It is not what you think it is. It's a true mathematical result. It is not what you think of as the CHSH inequality.

By the way,

(1) I don't think anyone should "use" it in the way you seem to mean by that word

(2) I can't explain how QM violates it

(3) It is trivial to understand how data might violate it

(4) The conclusion of my theorem need not hold if its assumptions do not hold. That explains why your simulation, Fred, does violate the inequality.

We will start with (4). The simulation NEVER EVER "violates" the inequality. Maybe some day you will get your head strapped on straight.

Number (1) is gibberish nonsense.

(2) Of course you can't explain how QM exceeds the inequality because it is freakin' IMPOSSIBLE. QM just ignores the inequality. Doesn't use it.

(3) Is just more freakin' nonsense.

Please demonstrate MATHEMATICALLY how QM or the experiments exceed the bounds on the CHSH inequality while using the CHSH inequality.

Of course I set you up with an impossible task and you are scratching your head about it.
.

Posted: **Fri Nov 12, 2021 9:28 pm**

FrediFizzx wrote: ↑Tue Nov 09, 2021 8:58 am We will start with (4). The simulation NEVER EVER "violates" the inequality. Maybe someday you will get your head strapped on straight.

Perhaps some explanation would be helpful here. For some strange reason, Gill seems to believe the simulation has something to do with some inequalities. Probably because we are somewhat following Bell's prescriptions for the A and B local functions. But those prescription are simply what you must do to construct local functions whether they be for QM or something more classical. Nothing really to do with the inequalities though Bell might have used them for such purpose.
.

Posted: **Sun Nov 14, 2021 12:05 am**

FrediFizzx wrote: ↑Fri Nov 12, 2021 9:28 pm
FrediFizzx wrote: ↑Tue Nov 09, 2021 8:58 am We will start with (4). The simulation NEVER EVER "violates" the inequality. Maybe someday you will get your head strapped on straight.
Perhaps some explanation would be helpful here. For some strange reason, Gill seems to believe the simulation has something to do with some inequalities. Probably because we are somewhat following Bell's prescriptions for the A and B local functions. But those prescription are simply what you must do to construct local functions whether they be for QM or something more classical. Nothing really to do with the inequalities though Bell might have used them for such purpose.

This is the math section of the forum. I derived a math theorem. In itself, it is a theorem about random variables and probability distributions and about conditional distributions. It is not “about” anything in physics or anything in computer science. It does have a connection to the mathematical ingredients in Bell’s arguments. That seems to confuse Fred.

I have used this math theorem to say something about some problems in computer science. We could talk about that on this forum, too. Maybe there should be a computer science section as well as a math section.

Simulations do not “use” inequalities. But one can prove mathematical theorems about what simulations can do, and can’t do. For instance, I have proved some theorems and applied them to Michel’s simulations. His simulation results, of course, agree with my theorems. A true theorem is of course a tautology.

Also, Fred’s simulation results agree with the relevant theorems.

Posted: **Sun Nov 14, 2021 12:41 am**

gill1109 wrote: ↑Sun Nov 14, 2021 12:05 am ... Also, Fred’s simulation results agree with the relevant theorems.

Double LOL! In your dreams you actually think they are math theorems when in fact they are junk math theories.

You still haven't demonstrated how QM or the experiments seem to "violate" or exceed the bounds on the inequalities when in fact no such thing ever happens. That right there should give you clue that your head is not strapped on quite correctly if you believe otherwise.

Now, you have to demonstrate that the simulations agree with your junk math theories!!!! Gotta see that math fiasco.

.

Posted: **Sun Nov 14, 2021 8:05 am**

FrediFizzx wrote: ↑Tue Nov 09, 2021 7:51 am @gill1109
Please demonstrate MATHEMATICALLY how QM or the experiments exceed the bounds on the CHSH inequality while using the CHSH inequality.

QM satisfies and can attain the Tsirelson inequality, $S \le 2 \sqrt 2$ .
Joy Christian also derives this same inequality in his framework.
The CHSH inequality is $S \le 2$ .
The experiments confirm QM.
They do not “use” any inequality.
QM does not”use” any inequality.
I hope you understand that $2 < 2\sqrt 2$

Those theorems are about theoretical correlations. If you like, about experiments with really huge numbers of trials.

In practice, observed correlations can deviate from their large N limit.

In principle one can easily get data (simulated or observed) with $S = 4$

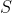
My 2001 paper https://arxiv.org/abs/quant-ph/0110137 is about distributed computing, about attempts to generate quantum correlations on a network of computers. I show that under certain conditions, the probability of observing a value of $S$ larger than 2 by any given amount is exponentially small in the number of trials.

I have the impression, Fred, that you do not know much about probability and statistics. If you would like anything explained, just go ahead and ask. Then you won’t have to keep asking meaningless questions.

Posted: **Sun Nov 14, 2021 4:02 pm**

gill1109 wrote: ↑Sun Nov 14, 2021 8:05 am
FrediFizzx wrote: ↑Tue Nov 09, 2021 7:51 am @gill1109
Please demonstrate MATHEMATICALLY how QM or the experiments exceed the bounds on the CHSH inequality while using the CHSH inequality.
QM satisfies and can attain the Tsirelson inequality, $S \le 2 \sqrt 2$ .
Joy Christian also derives this same inequality in his framework.
The CHSH inequality is $S \le 2$ .
The experiments confirm QM.
They do not “use” any inequality.
QM does not”use” any inequality.
I hope you understand that $2 < 2\sqrt 2$

Those theorems are about theoretical correlations. If you like, about experiments with really huge numbers of trials.

In practice, observed correlations can deviate from their large N limit.

In principle one can easily get data (simulated or observed) with $S = 4$

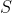
My 2001 paper https://arxiv.org/abs/quant-ph/0110137 is about distributed computing, about attempts to generate quantum correlations on a network of computers. I show that under certain conditions, the probability of observing a value of $S$ larger than 2 by any given amount is exponentially small in the number of trials.

Man o' man, you really don't have any freakin' clue at all do you? Or..., just being freakin' dishonest as hell!!! I guess I will have demonstrate how QM and the experiments cheat when they claim they have "violated" or exceeded the bound(s) of such an inequality. We will use CHSH as it is the most common inequality. It is pretty easy to see that if the 4 terms in the inequality are independent, the bound is 4 instead of 2 when some of the terms are dependent on each other which we demonstrate as +1 +1 - (-1) +1 = 4. And easy to see what happens in the case of quantum mechanics. Because of the negative cosine curve prediction, you are limited to using approx. +/- 0.707 per term instead of +/-1 and we demonstrate again as 0.707 + 0.707 - (- 0.707) + 0.707 = $2\sqrt{2}$ .

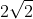
So, we see already that QM is capable of having a result greater than 2. Well..., how is that possible? Very simple! QM breaks the dependencies that give the CHSH bound result as 2. Same with the experimenters. IOW, they are NOT using the CHSH inequality that gives us such a bound as 2. Cheating!!! Now, the breaking of the dependencies have been thoroughly explained professionally by Michel, Joy, me and others so you all can look it up on the old forum. Perhaps a new expose' is called for on our new forum. But here is the absolute KILLER for the Bell nonsense. It is mathematically impossible for ANYTHING to "violate" or exceed the bounds on the inequality when using that inequality!!! QED. And that is how we know the Bell Fanatics are talking complete B**LS**T!!!

.

Posted: **Sun Nov 14, 2021 9:20 pm**

Fred, this thread is about mathematics, not about arithmetic.

In Bell’s mathematical model of Local Realism, the four terms are not independent. They depend on the same four mathematical functions A(a, .), A(a’, .), B(b, .), B(b’, .) on the same Kolmogorovian probability space (Omega, F, P).

In Tsirelson’s mathematical proof of his famous inequality, the four terms are not independent. They depend on the same four observables (self-adjoint operators) A, A’, B, B’ and the same quantum state rho on the same Hilbert space H.

When Tsirelson’s observables commute, his model is fully equivalent to Bell’s model. Four commuting observables correspond to four Kolmogorovian random variables, and vice versa. QM allows strictly more to be possible than LR.

QM allows many more possibilities than just the negative cosine curve.

LR allows many more possibilities than just the triangle wave.

That was about two competing mathematical theories which tell us what possibilities there are within the relevant theory for four theoretical correlations, which are assumed not to be independent of one another!

Experiment is yet another matter. Finite data sets can produce any four correlations you like (just as long as they are rational numbers). But what the hell, who cares! “Real numbers” are just mathematical fictions. They don’t really exist.

Sci.Physics.Foundations

A theorem in probability theory

A theorem in probability theory

Re: A theorem in probability theory

Re: A theorem in probability theory

Re: A theorem in probability theory

Re: A theorem in probability theory

Re: A theorem in probability theory

Re: A theorem in probability theory

Re: A theorem in probability theory

Re: A theorem in probability theory

Re: A theorem in probability theory

Re: A theorem in probability theory

Re: A theorem in probability theory

Re: A theorem in probability theory

Re: A theorem in probability theory

Re: A theorem in probability theory

Re: A theorem in probability theory

Re: A theorem in probability theory

Re: A theorem in probability theory

Re: A theorem in probability theory

Re: A theorem in probability theory