Sci.Physics.Foundations

.
I have written a new paper exposing the falsehood of Bell's theorem. It demonstrates where Bell's conceptual mistake originated from:

Symmetric Derivation of the Singlet Correlations within a Quaternionic 3-sphere, DOI: http://dx.doi.org/10.13140/RG.2.2.15725.46565

Abstract: We present a symmetric derivation of the strong correlations predicted by the entangled singlet state in a local-realistic model in which the physical space is assumed to be a quaternionic 3-sphere, or $S^3$, available as the spatial part of a solution of Einstein's field equations of general relativity, and compare it with Bell's local model for the singlet correlations set within a flat Euclidean space ${\mathrm{I\!R}^3}$. Since the probabilities of observing measurement outcomes for Bell's local model have never been fully worked out before, our analysis may also provide useful comparisons for other less compelling models, such as those relying on retrocausality and superdeterminism. Apart from the conservation of spin angular momentum, the key attribute underlying the strong singlet correlations within $S^3$ turns out to be the spinorial sign changes intrinsic to the quaternions that constitute the 3-sphere. We also discuss anew a macroscopic experiment that can, in principle, test the 3-sphere hypothesis.

Here is what is new in this paper:

(1) I have not used the orientation lambda as a hidden variable. This eliminates some unfounded objections to it, such as those by Gill and Lasenby.

(2) With lambda gone, there are no grounds for another unfounded claim by Gill, that AB = -1 in the model regardless of the settings a and b.

(3) I explicitly bring out the mistake made by Bell and Peres in their computation of correlations within the original Bell's local model of 1964.

(4) I do not use the rotation axis r_0, or show that it vanishes in the measurement limits (most likely this point is of interest to Fred Diether).

(5) I discuss in more detail my proposed macroscopic experiment (originally published in 2015) to test the physical relevance of Bell's theorem.

(6) The derivation of the strong singlet correlations is now simpler, completely clean, and unambiguous (just like all of my previous derivations).

Finally, in anticipation of another unfounded objection, note that conservation of spin angular momentum holds only for the free evolutions of the spins. The conservation law does not hold during the physical interactions that take place during the detection processes at the two ends of the experiment.
.

Joy Christian wrote: ↑Tue Apr 19, 2022 12:19 am ...

(4) I do not use the rotation axis r_0, or show that it vanishes in the measurement limits (most likely this point is of interest to Fred Diether).
...

Well, I do like the r_0 method since the limits actually get taken instead of just dropping out. But there is nothing wrong with the limits dropping out in the product calculation. And it is easier to understand. I already partially have the simulation for verification done. I will clean it up and post it later.
.

Here is a simple version of the simulation for verification of eqs. (49) to (57).

sims/S3_GA_forum.pdf
sims/S3_GA_forum.nb
.

FrediFizzx wrote: ↑Tue Apr 19, 2022 10:44 am Here is a simple version of the simulation for verification of eqs. (49) to (57).

sims/S3_GA_forum.pdf
sims/S3_GA_forum.nb

Brilliant! Thanks!
.

Joy Christian wrote: ↑Tue Apr 19, 2022 11:11 am

FrediFizzx wrote: ↑Tue Apr 19, 2022 10:44 am Here is a simple version of the simulation for verification of eqs. (49) to (57).

sims/S3_GA_forum.pdf
sims/S3_GA_forum.nb

Brilliant! Thanks!

You're welcome. I forgot to mention that the simulation is using the particle physics version of the conservation of angular momentum. It gets rid of the ad hoc minus signs.
.

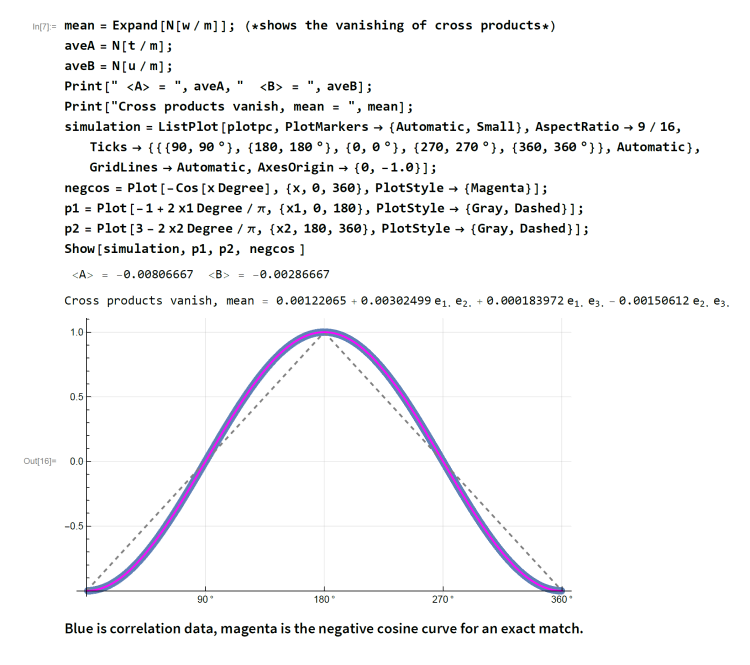
The simulation is short enough so we can just post it as a picture.



.

.
The paper is now also available from the physics arXiv with a DOI: https://doi.org/10.48550/arXiv.2204.10288.
.

Well done!

["Never give up, never surrender" - Galaxy Quest]

FrediFizzx wrote: ↑Tue Apr 19, 2022 6:35 pm The simulation is short enough so we can just post it as a picture.

Oops! I made a mistake. The cross product cancelation is exact. I'll post a correction tomorrow. GeometricProduct[ag, bg] should be GeometricProduct[bg, ag].
.

I will just post the correction and result.



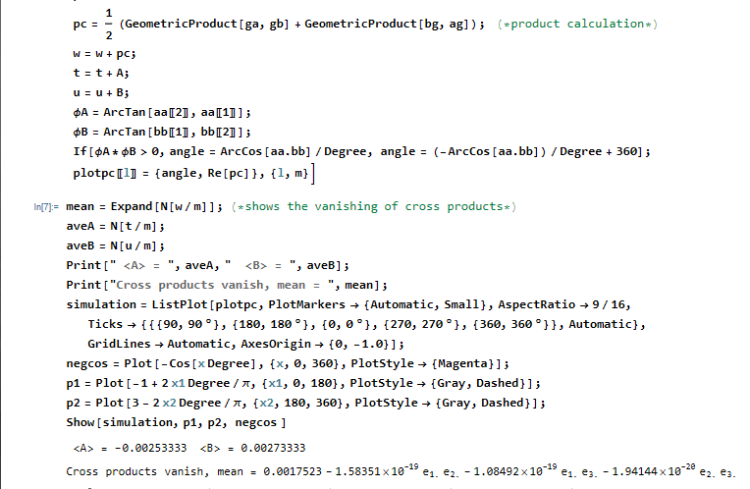
But it looks like we have some rounding error in the calculation so if we post one event we can see the exact cancelation of the cross products.



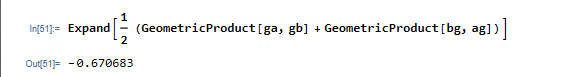
Another Mathematica mystery is why it puts a decimal point after e_1., e_2., etc.
.

Using quaternions and 2D vectors, Mathematica does the cross product cancelation exact.



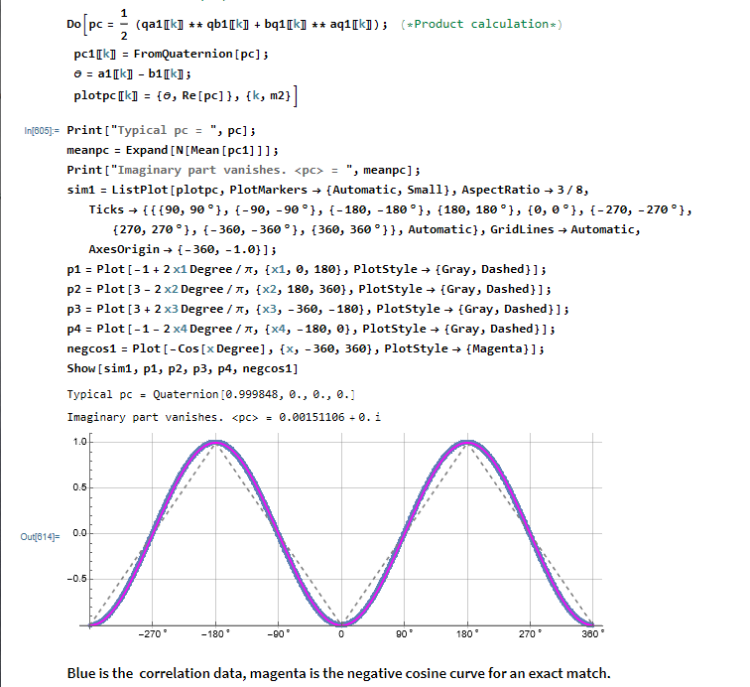
However, it seems a bit strange to have AB and BA happening at the same time. Are we mixing the right handed view with the left handed view? I have to say that the r_0 method of cross product cancelation is superior though more complicated.
.

FrediFizzx wrote: ↑Sat Apr 30, 2022 5:54 am However, it seems a bit strange to have AB and BA happening at the same time. Are we mixing the right handed view with the left handed view? I have to say that the r_0 method of cross product cancelation is superior though more complicated.

AB = 1/2 { AB + BA } is a mathematical identity for scalars such as A = +/-1 and B = +/-1. So 1/2 { AB + BA } allows us to produce a scalar -cos(a, b) in the calculation without having to consider the right-handed and left-handed views. The r_0 method is also fine. I just wanted to make the calculation simpler.
.

Joy Christian wrote: ↑Sat Apr 30, 2022 6:48 am

FrediFizzx wrote: ↑Sat Apr 30, 2022 5:54 am However, it seems a bit strange to have AB and BA happening at the same time. Are we mixing the right handed view with the left handed view? I have to say that the r_0 method of cross product cancelation is superior though more complicated.

AB = 1/2 { AB + BA } is a mathematical identity for scalars such as A = +/-1 and B = +/-1. So 1/2 { AB + BA } allows us to produce a scalar -cos(a, b) in the calculation without having to consider the right-handed and left-handed views. The r_0 method is also fine. I just wanted to make the calculation simpler.

Well, for it to be more physically realistic, you need to do something like this.



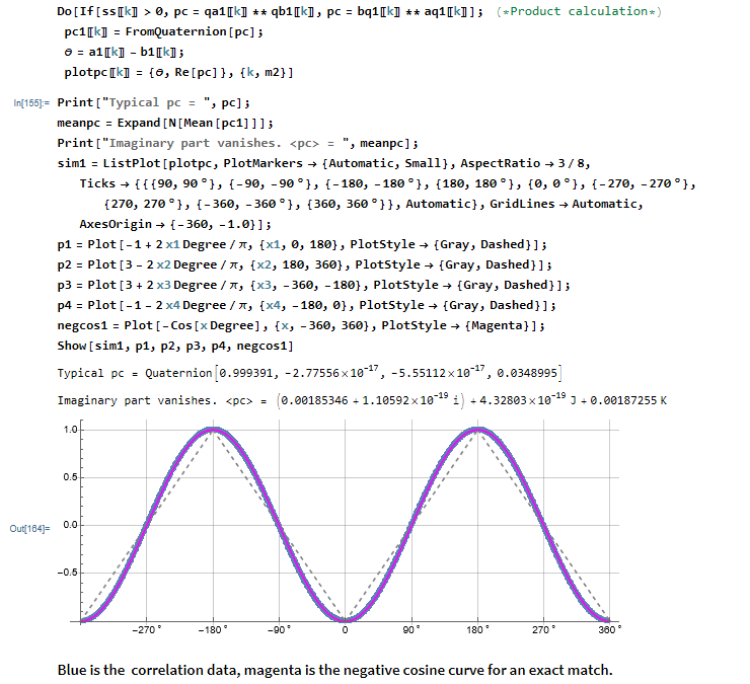
Where ss_k is a 2D angle derived from the 3D singlet spin vector, s. Of course the cross product cancelation is not exact but it still vanishes.
.

This also works with Ls1_k_4 > 0 which is the "z" component of the singlet spin vector. I think I will be using that. IOW, the left or right handedness of the product is randomly determined by the orientation of the singlet vector instead of independently by lambda = +/-1. Let's say that the axis of propagation for the two particles is "z" with A being the plus direction from the origin and B the minus direction, then if the "z" component is pointing toward A the order is AB. If pointing toward B the order is BA.
.

Joy, you define your measurement outcomes in (13) and (19). This involves limits: limits as s_1 converges to mu_1 a, and as s_2 converges to mu_2 b. But mu_1 and mu_2 are not fixed, in fact they are defined in terms of s_1 and s_2, see (11): mu_1 = sign(a . s_1) and mu_2 = sign(s_2 . b)

gill1109 wrote: ↑Sun May 01, 2022 10:56 pm
Joy, you define your measurement outcomes in (13) and (19). This involves limits: limits as s_1 converges to mu_1 a, and as s_2 converges to mu_2 b. But mu_1 and mu_2 are not fixed, in fact they are defined in terms of s_1 and s_2, see (11): mu_1 = sign(a . s_1) and mu_2 = sign(s_2 . b)

That is not correct. In eq. (11) mu_1 and mu_2 are defined to be fixed for each run. They are defined in terms of the initial spin direction s^i at the source.

It is important to read what I have defined carefully.
.

Joy Christian wrote: ↑Sun May 01, 2022 11:35 pm

gill1109 wrote: ↑Sun May 01, 2022 10:56 pm
Joy, you define your measurement outcomes in (13) and (19). This involves limits: limits as s_1 converges to mu_1 a, and as s_2 converges to mu_2 b. But mu_1 and mu_2 are not fixed, in fact they are defined in terms of s_1 and s_2, see (11): mu_1 = sign(a . s_1) and mu_2 = sign(s_2 . b)

That is not correct. In eq. (11) mu_1 and mu_2 are defined to be fixed for each run. They are defined in terms of the initial spin direction s^i at the source.

It is important to read what I have defined carefully.

LOL! I doubt that is ever going to happen in Gill's case. It is quite mind boggling that someone has such trouble with something that is soooo... simple.
.

Here is an alternative simple GA simulation. I realized last night that we don't really know if particle 1 goes to A or B. Likewise for particle 2 so, I have switched the spin representation in the reverse order to show that it doesn't matter. And this simulation is using the direction of the "z" component of the singlet spin vector for the reverse order of the product.




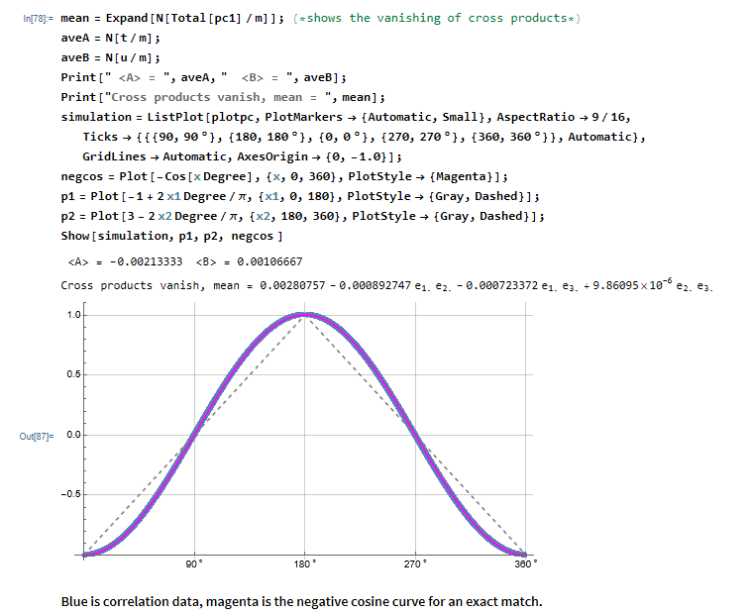
Now, we have the QM prediction in a classical local way with no hidden variable and we also have shown that QM is local for the -a.b prediction with no hidden variable. So, where does that leave Bell and his hidden variable program? Out in the very cold with the realization that what he did was complete BS. You're welcome.
.

Joy Christian wrote: ↑Sun May 01, 2022 11:35 pm

gill1109 wrote: ↑Sun May 01, 2022 10:56 pm
Joy, you define your measurement outcomes in (13) and (19). This involves limits: limits as s_1 converges to mu_1 a, and as s_2 converges to mu_2 b. But mu_1 and mu_2 are not fixed, in fact they are defined in terms of s_1 and s_2, see (11): mu_1 = sign(a . s_1) and mu_2 = sign(s_2 . b)

That is not correct. In eq. (11) mu_1 and mu_2 are defined to be fixed for each run. They are defined in terms of the initial spin direction s^i at the source.

It is important to read what I have defined carefully.
.

OK, but in that case the notation and/or explanation needs some improvement. You are using s^1 twice in the same expression (once explicitly, once implicitly), and similar for s^2, but the two occurrences are not supposed to be the same.

You must also define the initial two spin directions.

gill1109 wrote: ↑Sun May 08, 2022 2:43 am

Joy Christian wrote: ↑Sun May 01, 2022 11:35 pm

gill1109 wrote: ↑Sun May 01, 2022 10:56 pm
Joy, you define your measurement outcomes in (13) and (19). This involves limits: limits as s_1 converges to mu_1 a, and as s_2 converges to mu_2 b. But mu_1 and mu_2 are not fixed, in fact they are defined in terms of s_1 and s_2, see (11): mu_1 = sign(a . s_1) and mu_2 = sign(s_2 . b)

That is not correct. In eq. (11) mu_1 and mu_2 are defined to be fixed for each run. They are defined in terms of the initial spin direction s^i at the source.

It is important to read what I have defined carefully.
.

OK, but in that case the notation and/or explanation needs some improvement. You are using s^1 twice in the same expression (once explicitly, once implicitly), and similar for s^2, but the two occurrences are not supposed to be the same.

You must also define the initial two spin directions.

Either you are getting too old for this stuff or your eyesight needs checking. Or maybe you just don't read stuff anymore. Please read my paper or my above comment again. What I have used to define mu_1 and mu_2 is the initial spin direction s^i, not s_1 or s_2. Here the superscript "i" refers to the initial spin direction at the source, and the subscripts 1 and 2 refer to the observation stations at the two ends of the experiment. This is not difficult to understand.
.