Page 1 of 1
Joint Probabilities of Results in Bell’s Local Model
Posted: Fri Nov 05, 2021 3:05 pm
by Joy Christian
.
For fun, I have worked out the joint probabilities of observing various results in Bell’s local model for the singlet correlations. It was a trivial exercise, but I don’t think anyone has bothered to work them out until now. They are instructive to reflect on and may be useful for comparing different models.
Here is the two-page paper:
http://dx.doi.org/10.13140/RG.2.2.29315.84004
.
Re: Joint Probabilities of Results in Bell’s Local Model
Posted: Fri Nov 05, 2021 3:42 pm
by Justo
I suppose that equation (1) is not "Bell's model" in general. Is one possible "local realistic" model. Right?
Re: Joint Probabilities of Results in Bell’s Local Model
Posted: Fri Nov 05, 2021 3:44 pm
by Joy Christian
Justo wrote: ↑Fri Nov 05, 2021 3:42 pm
I suppose that equation (1) is not "Bell's model" in general. Is one possible "local realistic" model. Right?
No. Eq. (1) is Bell's local model. See Section 3 of his 1964 paper.
.
Re: Joint Probabilities of Results in Bell’s Local Model
Posted: Fri Nov 05, 2021 3:54 pm
by Justo
Joy Christian wrote: ↑Fri Nov 05, 2021 3:44 pm
Justo wrote: ↑Fri Nov 05, 2021 3:42 pm
I suppose that equation (1) is not "Bell's model" in general. Is one possible "local realistic" model. Right?
No. Eq. (1) is Bell's local model. See Section 3 of his 1964 paper.
.
I do not agree. See the title, it is only an illustration, an example of a local realistic model with
=const=\frac{1}{2\pi})
. I think that Gill wrote a paper exploring other possibilities where the "triangle line" is replaced by a more general zig-zag polygonal line.
Re: Joint Probabilities of Results in Bell’s Local Model
Posted: Fri Nov 05, 2021 4:00 pm
by Joy Christian
Justo wrote: ↑Fri Nov 05, 2021 3:54 pm
Joy Christian wrote: ↑Fri Nov 05, 2021 3:44 pm
Justo wrote: ↑Fri Nov 05, 2021 3:42 pm
I suppose that equation (1) is not "Bell's model" in general. Is one possible "local realistic" model. Right?
No. Eq. (1) is Bell's local model. See Section 3 of his 1964 paper.
I do not agree. See the title, it is only an illustration, an example of a local realistic model with
=const=\frac{1}{2\pi})
. I think that Gill wrote a paper exploring other possibilities where the "triangle line" is replaced by a more general zig-zag polygonal line.
Eq. (1) in my paper is known --- indeed well known --- as "Bell's local model." My paper is about probabilities in that specific "Bell's local model."
.
Re: Joint Probabilities of Results in Bell’s Local Model
Posted: Fri Nov 05, 2021 4:25 pm
by FrediFizzx
Justo wrote: ↑Fri Nov 05, 2021 3:42 pm
I suppose that equation (1) is not "Bell's model" in general. Is one possible "local realistic" model. Right?
There you go with that "in general" nonsense again. Eq. (1)
IS Bell's model period!! And................. we actually use it in our soon to be extremely famous local-realistic simulation.
http://www.sciphysicsforums.com/spfbb1/ ... 780#p15228
In fact, we use it twice with two different HV mechanisms tied back to his single lambda. Which is theta in our case. It's really quite awesome!!!!



.
Re: Joint Probabilities of Results in Bell’s Local Model
Posted: Fri Nov 05, 2021 10:33 pm
by gill1109
Justo wrote: ↑Fri Nov 05, 2021 3:54 pm
Joy Christian wrote: ↑Fri Nov 05, 2021 3:44 pm
Justo wrote: ↑Fri Nov 05, 2021 3:42 pm
I suppose that equation (1) is not "Bell's model" in general. Is one possible "local realistic" model. Right?
No. Eq. (1) is Bell's local model. See Section 3 of his 1964 paper.
.
I do not agree. See the title, it is only an illustration, an example of a local realistic model with
=const=\frac{1}{2\pi})
. I think that Gill wrote a paper exploring other possibilities where the "triangle line" is replaced by a more general zig-zag polygonal line.
Exactly. It’s the most simple local model you can think of with certain characteristics (perfect anticorrelation at equal settings). But one can easily explore all possible ones. Some of them even have some correlations “outside” of the triangle wave.
https://arxiv.org/abs/1312.6403
It has lots of nice pictures!
The triangle wave versus the cosine: How classical systems can optimally approximate EPR-B correlations
The famous singlet correlations of a composite quantum system consisting of two spatially separated components exhibit notable features of two kinds. The first kind consists of striking certainty relations: perfect correlation and perfect anti-correlation in certain settings. The second kind consists of a number of symmetries, in particular, invariance under rotation, as well as invariance under exchange of components, parity, or chirality. In this note, I investigate the class of correlation functions that can be generated by classical composite physical systems when we restrict attention to systems which reproduce the certainty relations exactly, and for which the rotational invariance of the correlation function is the manifestation of rotational invariance of the underlying classical physics. I call such correlation functions classical EPR-B correlations. It turns out that the other three (binary) symmetries can then be obtained "for free": they are exhibited by the correlation function, and can be imposed on the underlying physics by adding an underlying randomisation level. We end up with a simple probabilistic description of all possible classical EPR-B correlations in terms of a "spinning coloured disk" model, and a research programme: describe these functions in a concise analytic way. We survey open problems, and we show that the widespread idea that "quantum correlations are more extreme than classical physics allows" is at best highly inaccurate, through giving a concrete example of a classical correlation which satisfies all the symmetries and all the certainty relations and which exceeds the quantum correlations over a whole range of settings
Re: Joint Probabilities of Results in Bell’s Local Model
Posted: Sat Nov 06, 2021 3:12 am
by Joy Christian
gill1109 wrote: ↑Fri Nov 05, 2021 10:33 pm
Justo wrote: ↑Fri Nov 05, 2021 3:54 pm
Joy Christian wrote: ↑Fri Nov 05, 2021 3:44 pm
No. Eq. (1) is Bell's local model. See Section 3 of his 1964 paper.
.
I do not agree. See the title, it is only an illustration, an example of a local realistic model with
=const=\frac{1}{2\pi})
. I think that Gill wrote a paper exploring other possibilities where the "triangle line" is replaced by a more general zig-zag polygonal line.
Exactly. It’s the most simple local model you can think of with certain characteristics (perfect anticorrelation at equal settings). But one can easily explore all possible ones. Some of them even have some correlations “outside” of the triangle wave.
New forum, but the same old spewing of nonsense. For heaven's sake, my two-page paper is about "Bell's local model" from his 1964 paper. I am not concerned about any other model in my paper. Do correct me if anyone else has worked out the probabilities P(++), etc., for Bell's local model of 1964.
.
Re: Joint Probabilities of Results in Bell’s Local Model
Posted: Sat Nov 06, 2021 4:25 am
by Justo
Joy Christian wrote: ↑Sat Nov 06, 2021 3:12 am
New forum, but the same old spewing of nonsense. For heaven's sake, my two-page paper is about "Bell's local model" from his 1964 paper. I am not concerned about any other model in my paper. Do correct me if anyone else has worked out the probabilities P(++), etc., for Bell's local model of 1964.
.
Joy, I think the problem is the way you express it. You say "Bell's local model" meaning Bell's illustration in his 1964 paper. So it seems that his theorem only applies to his illustration and not to arbitrary functions A(lambda, a), B(lambda, b), and rho(lambda).
Of course, I know you reject the theorem but to claim that it only applies to his illustrative example is new to me.
Re: Joint Probabilities of Results in Bell’s Local Model
Posted: Sat Nov 06, 2021 4:39 am
by Joy Christian
Justo wrote: ↑Sat Nov 06, 2021 4:25 am
Joy Christian wrote: ↑Sat Nov 06, 2021 3:12 am
New forum, but the same old spewing of nonsense. For heaven's sake, my two-page paper is about "Bell's local model" from his 1964 paper. I am not concerned about any other model in my paper. Do correct me if anyone else has worked out the probabilities P(++), etc., for Bell's local model of 1964.
.
Joy, I think the problem is the way you express it. You say "Bell's local model" meaning Bell's illustration in his 1964 paper. So it seems that his theorem only applies to his illustration and not to arbitrary functions A(lambda, a), B(lambda, b), and rho(lambda).
Of course, I know you reject the theorem but to claim that it only applies to his illustrative example is new to me.
.
That is not the claim. Both you and Gill are not experts in the foundations of quantum mechanics. That is why both of you are confused. All experts in foundations of quantum mechanics, such as myself, my Ph.D. mentor Abner Shimony, his collaborator Mike Horne, my former colleagues and friends such as Lucien Hardy, Antony Valentini, and some of the current occupants of Perimeter Institute, instantly understand what is meant by "Bell's local model." If you and Gill are confused by the terminology, then that is entirely your problem. Moreover, it is quite clear from the introduction in my paper what I am talking about.
.
Re: Joint Probabilities of Results in Bell’s Local Model
Posted: Sat Nov 06, 2021 5:20 am
by FrediFizzx
And... I'm no expert in the foundations of QM, but I also instantly understood what Joy was talking about. Especially since it is used twice in the simulation.
.
Re: Joint Probabilities of Results in Bell’s Local Model
Posted: Sat Nov 06, 2021 6:58 am
by gill1109
Joy Christian wrote: ↑Fri Nov 05, 2021 4:00 pm
Justo wrote: ↑Fri Nov 05, 2021 3:54 pm
Joy Christian wrote: ↑Fri Nov 05, 2021 3:44 pm
No. Eq. (1) is Bell's local model. See Section 3 of his 1964 paper.
I do not agree. See the title, it is only an illustration, an example of a local realistic model with
=const=\frac{1}{2\pi})
. I think that Gill wrote a paper exploring other possibilities where the "triangle line" is replaced by a more general zig-zag polygonal line.
Eq. (1) in my paper is known --- indeed well known --- as "Bell's local model." My paper is about probabilities in that specific "Bell's local model."
I agree. Bell has a specific model which he introduces as an example, and he also has a family of models. The specific model is well known as Bell's local model (or something very similar). But obviously, confusion is possible, since we also have Bell's general formulation of local hidden variables.
I also do not know if the probabilities which Joy refers to have been calculated before. However, if one knows the correlation and the two marginal distributions of the outcomes then you know all four probabilities of the outcome pairs ++, +-, -+, --. This is true, because of the following considerations.
All four probabilities add to one.
The probabilities of ++ and of +- add to 0.5.
The probabilities of ++ and of -+ add to 0.5.
The correlation is the probability of equal outcomes minus the probability of unequal outcomes.
That gives us four linear relations with four unknowns (if the correlation is already known). Not difficult to solve.
Denote the correlation by "r"
(P(++) + P(--)) - (P(+-) + P(--)) = r
But
(P(++) + P(--)) + (P(+-) + P(--)) = 1
So
P(++) + P(--) = (1 + r) / 2
By symmetry,
P(++) = P(--)
Therefore
P(++) = P(--) = (1 + r) / 4
P(+-) = P(-+) = (1 - r) / 4
Hence P(++) +
Re: Joint Probabilities of Results in Bell’s Local Model
Posted: Sat Nov 06, 2021 7:23 am
by gill1109
Denote the correlation by "r". This tells us
 + P(--)) - (P(+-) + P(--)) = r.)
But
 + P(--)) + (P(+-) + P(--)) = 1.)
So (add the equations, divide by 2)
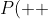 + P(--) = (1 + r) / 2.)
By symmetry (can also be proven by similar linear algebra),
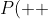 = P(--).)
Therefore we find all four probabilities
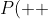 = P(--) = (1 + r) / 4,)
 = P(-+) = (1 - r) / 4.)
Check: for "r" between -1 and +1, that gives us four probabilities which add up to one, and with Alice's and Bob's marginal probabilities of "+" both equal to 0.5. There can be no other solution with the same value of the correlation "r".
Re: Joint Probabilities of Results in Bell’s Local Model
Posted: Sat Nov 06, 2021 7:45 am
by FrediFizzx
gill1109 wrote: ↑Sat Nov 06, 2021 7:23 am
Denote the correlation by "r". This tells us
 + P(--)) - (P(+-) + P(--)) = r.)
But
 + P(--)) + (P(+-) + P(--)) = 1.)
So (add the equations, divide by 2)
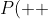 + P(--) = (1 + r) / 2.)
By symmetry (can also be proven by similar linear algebra),
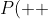 = P(--).)
Therefore we find all four probabilities
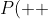 = P(--) = (1 + r) / 4,)
 = P(-+) = (1 - r) / 4.)
Check: for "r" between -1 and +1, that gives us four probabilities which add up to one, and with Alice's and Bob's marginal probabilities of "+" both equal to 0.5. There can be no other solution with the same value of the correlation "r".
And for our simulations that cover the range of 0 to 360 degrees in 1 degree increments, r is going to be pretty close to zero every time.
.
Re: Joint Probabilities of Results in Bell’s Local Model
Posted: Sat Nov 06, 2021 8:54 am
by Joy Christian
FrediFizzx wrote: ↑Sat Nov 06, 2021 7:45 am
gill1109 wrote: ↑Sat Nov 06, 2021 7:23 am
Denote the correlation by "r". This tells us
 + P(--)) - (P(+-) + P(--)) = r.)
But
 + P(--)) + (P(+-) + P(--)) = 1.)
So (add the equations, divide by 2)
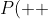 + P(--) = (1 + r) / 2.)
By symmetry (can also be proven by similar linear algebra),
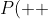 = P(--).)
Therefore we find all four probabilities
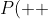 = P(--) = (1 + r) / 4,)
 = P(-+) = (1 - r) / 4.)
Check: for "r" between -1 and +1, that gives us four probabilities which add up to one, and with Alice's and Bob's marginal probabilities of "+" both equal to 0.5. There can be no other solution with the same value of the correlation "r".
And for our simulations that cover the range of 0 to 360 degrees in 1 degree increments, r is going to be pretty close to zero every time.
The comparison of the simulation with Bell's local model is instructive.
In the simulation: < P(++) > = < P(--) > = < P(+-) > = < P(-+) > = 0.25, where <...> is average over the angle eta between a and b.
In Bell's local model, on the other hand, these averages are dramatically different, but still add up to 1, just like in the simulation:
For 0 < eta < pi, < P(++) > = < P(--) > = 0 and < P(+-) > = < P(-+) > = +0.5, so the four quantities add up to 1.
For pi < eta < 2pi, < P(++) > = < P(--) > = 1 and < P(+-) > = < P(-+) > = -0.5, so the four quantities again add up to 1.
.
Re: Joint Probabilities of Results in Bell’s Local Model
Posted: Sat Nov 06, 2021 9:19 am
by gill1109
FrediFizzx wrote: ↑Sat Nov 06, 2021 7:45 am
gill1109 wrote: ↑Sat Nov 06, 2021 7:23 am
Denote the correlation by "r". This tells us
 + P(--)) - (P(+-) + P(--)) = r.)
But
 + P(--)) + (P(+-) + P(--)) = 1.)
So (add the equations, divide by 2)
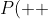 + P(--) = (1 + r) / 2.)
By symmetry (can also be proven by similar linear algebra),
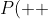 = P(--).)
Therefore we find all four probabilities
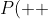 = P(--) = (1 + r) / 4,)
 = P(-+) = (1 - r) / 4.)
Check: for "r" between -1 and +1, that gives us four probabilities which add up to one, and with Alice's and Bob's marginal probabilities of "+" both equal to 0.5. There can be no other solution with the same value of the correlation "r".
And for our simulations that cover the range of 0 to 360 degrees in 1 degree increments, r is going to be pretty close to zero every time.
.
Fred,
In Joy's new note, he is talking about P(++| a, b).
That's different from P(++).
Sorry, I should have added the settings in my notation. Given a and b, the correlation is *not* zero. I should have written P(++ | a, b) and so on.
EPR-B QM standard calculations, and your simulation, gets the negative cosine. Bell's simple local model gets the triangle wave. More complex local models can get all kinds of things (see my paper with lots of simulations and lots of pictures).
Re: Joint Probabilities of Results in Bell’s Local Model
Posted: Sat Nov 06, 2021 9:22 am
by gill1109
Notation corrected: Denote the correlation, for given settings
a,
b, by
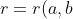.)
This tells us
 + P(--|a,b)) - (P(+-|a,b) + P(--|a,b)) = r.)
But
 + P(--|a,b)) + (P(+-|a,b) + P(--|a,b)) = 1.)
So (add the equations, divide by 2)
 + P(--|a,b) = (1 + r) / 2.)
By symmetry (can also be proven by similar linear algebra, from what we already know),
 = P(--|a,b).)
Therefore we find all four probabilities
 = P(--|a,b) = (1 + r) / 4,)
 = P(-+|a,b) = (1 - r) / 4.)
I suppose that this corresponds to what Joy found in his new short paper.