First we will take this latest one that I posted.
download/newCS-35-S3quat-prodcalc-forum.pdf
Basically similar to Joy's original. Does anyone have trouble with the first section? Speak up if you do. But doubtful any of the Bell fanatics will read and/or want to understand it since it destroys their Bell world.
Load Quaternion Package, Set Run Time Parameters, Initialize Arrays and Tables
We load the quaternion package so that Mathematica knows with to do with them. The next 5 lines are from John Reed and they just get it setup so that the coefficients of vectors can be integrated into the quaternion scheme. Then of course trial numbers and the number of trial degrees is self explanatory. The ConstantArrays and Tables are placeholders for upcoming data. Then we have,
Generating Particle Data with Three Independent Do-Loops
A Do-loop just does iterations on everything for the number of trials. We can see in the first Do-loop the generation of the singlet vector angle which is later incorporated into two quaternions. Ls1 and Ls2. These are the two particles that are to be detected by the A and B stations. Then we also have the two hidden variable mechanisms that are both tied back to "e" the singlet vector angle.
Then the A and B Do-loops do the same thing for each so we will just explain the A station. The "a" angle is just generated as a random integer. This helps to facilitate doing the (a-b) angle later at one degree increments but notice that the "e" vector is a random real angle. Then some manipulation is done to get the "a" angle into a quaternion which will be an X-Y 2D quaternion called Da. Then Da is iterated into a list Da1 for later use.
Also we form the quaternion qa from Da and Ls1 for later use in the If statement. Then the If statement selects A to be sign of the cosine of the angle between Da and Ls1 if greater than the HV value from the HV mechanism, else it is the sign of the sine of the angle between Da and Ls1. Also notice the limit replacement functions for the main part of A. Just like Joy has in his model. Next is putting together outA which is a table that contains the value for "a" and the value for A. And for B just replace all "a's" for "b's", B for A and Ls2 for Ls1.
Product Calculation
First we extract the values for a, b, A and B into lists that have all values for all the events. Then, q, s, t, and u are set to zero initial value for later use. Then we Do the product calculation along with the limit replacement functions. The calculation is reversed if lambda2 = -1. This is necessary for the cancelation of the imaginary terms generated by the product calculation. The cancellation can be seen as Meanq. Then (a1-b1) is set as a iteration called "angle". Next we have calculations for s, t, and u that will give us Meanq, the average of A and the average of B. Then we form plotq that is a table that contains the "angle" and the real part of the resultant quaternion from the product calculation as Re[q]. Next we print the values for the averages and do a ListPlot of the list plotq and compare those values with the negative cosine curve in the plot.
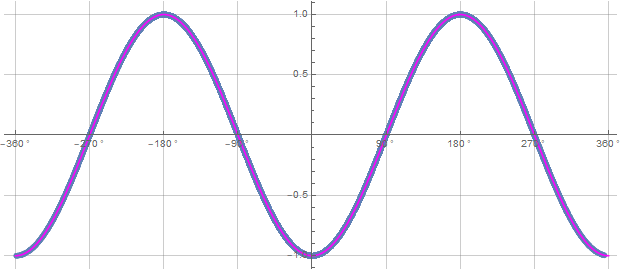 The blue is data points and the magenta is the -cosine curve for an exact match so easy to see that the model predicts -cos(a-b) exactly like quantum mechanics.
The blue is data points and the magenta is the -cosine curve for an exact match so easy to see that the model predicts -cos(a-b) exactly like quantum mechanics.
And that is it. If any questions or more details you would like to see, just ask.
First we will take this latest one that I posted.
https://sciphysicsfoundations.com/download/newCS-35-S3quat-prodcalc-forum.pdf
Basically similar to Joy's original. Does anyone have trouble with the first section? Speak up if you do. But doubtful any of the Bell fanatics will read and/or want to understand it since it destroys their Bell world.
[b]Load Quaternion Package, Set Run Time Parameters, Initialize Arrays and Tables[/b]
We load the quaternion package so that Mathematica knows with to do with them. The next 5 lines are from John Reed and they just get it setup so that the coefficients of vectors can be integrated into the quaternion scheme. Then of course trial numbers and the number of trial degrees is self explanatory. The ConstantArrays and Tables are placeholders for upcoming data. Then we have,
[b]Generating Particle Data with Three Independent Do-Loops[/b]
A Do-loop just does iterations on everything for the number of trials. We can see in the first Do-loop the generation of the singlet vector angle which is later incorporated into two quaternions. Ls1 and Ls2. These are the two particles that are to be detected by the A and B stations. Then we also have the two hidden variable mechanisms that are both tied back to "e" the singlet vector angle.
Then the A and B Do-loops do the same thing for each so we will just explain the A station. The "a" angle is just generated as a random integer. This helps to facilitate doing the (a-b) angle later at one degree increments but notice that the "e" vector is a random real angle. Then some manipulation is done to get the "a" angle into a quaternion which will be an X-Y 2D quaternion called Da. Then Da is iterated into a list Da1 for later use.
Also we form the quaternion qa from Da and Ls1 for later use in the If statement. Then the If statement selects A to be sign of the cosine of the angle between Da and Ls1 if greater than the HV value from the HV mechanism, else it is the sign of the sine of the angle between Da and Ls1. Also notice the limit replacement functions for the main part of A. Just like Joy has in his model. Next is putting together outA which is a table that contains the value for "a" and the value for A. And for B just replace all "a's" for "b's", B for A and Ls2 for Ls1.
[b]Product Calculation[/b]
First we extract the values for a, b, A and B into lists that have all values for all the events. Then, q, s, t, and u are set to zero initial value for later use. Then we Do the product calculation along with the limit replacement functions. The calculation is reversed if lambda2 = -1. This is necessary for the cancelation of the imaginary terms generated by the product calculation. The cancellation can be seen as Meanq. Then (a1-b1) is set as a iteration called "angle". Next we have calculations for s, t, and u that will give us Meanq, the average of A and the average of B. Then we form plotq that is a table that contains the "angle" and the real part of the resultant quaternion from the product calculation as Re[q]. Next we print the values for the averages and do a ListPlot of the list plotq and compare those values with the negative cosine curve in the plot.
[img]https://sciphysicsfoundations.com/download/Joys_prodcalc20K1.png[/img]
[b]The blue is data points and the magenta is the -cosine curve for an exact match so easy to see that the model predicts -cos(a-b) exactly like quantum mechanics.[/b]
And that is it. If any questions or more details you would like to see, just ask.
