Page 3 of 10
Re: Re: Coming Soon!
Posted: Wed Nov 17, 2021 11:48 pm
by FrediFizzx
gill1109 wrote: ↑Wed Nov 17, 2021 10:23 pm
FrediFizzx wrote: ↑Wed Nov 17, 2021 11:58 am
FrediFizzx wrote: ↑Wed Nov 17, 2021 8:44 am
Ah, don't give up yet. Another clue. Two worthless procedures that were in the code that I corrected.

Too bad John copped out on us. I'm a little surprised that he didn't say anything about it before. Well..., he always seemed to be a little grumpy to me. But I learned a lot from John. R.I.P.

I don’t understand the theta1 and theta2, lambda1 and lambda2. It’s all got more complicated, not less.
I am still yearning for a version written in a regular programming language.
Yearn away. That is something John copped out on you about. You can still send him a private message on the old forum if no email address. Not sure he would respond to it. But anyways, it
is written in a regular programming language for thousands of people. Very easy to understand and very easy to learn. Wolfram has a massive website for finding out what you might want to know about Mathematica.
It has two hidden variable processes both generated by same initial state theta_k. But now for the answer. I had un-necessary "Do's" in the A and B Do-loops that I took out. That enabled to get rid of about 10 lines of code so less complicated. So it should be easier to understand now.
.
Re: Re: Coming Soon!
Posted: Thu Nov 18, 2021 5:32 am
by gill1109
FrediFizzx wrote: ↑Wed Nov 17, 2021 11:48 pm
gill1109 wrote: ↑Wed Nov 17, 2021 10:23 pm
FrediFizzx wrote: ↑Wed Nov 17, 2021 11:58 am
Too bad John copped out on us. I'm a little surprised that he didn't say anything about it before. Well..., he always seemed to be a little grumpy to me. But I learned a lot from John. R.I.P.

I don’t understand the theta1 and theta2, lambda1 and lambda2. It’s all got more complicated, not less.
I am still yearning for a version written in a regular programming language.
Yearn away. That is something John copped out on you about. You can still send him a private message on the old forum if no email address. Not sure he would respond to it. But anyways, it
is written in a regular programming language for thousands of people. Very easy to understand and very easy to learn. Wolfram has a massive website for finding out what you might want to know about Mathematica.
It has two hidden variable processes both generated by same initial state theta_k. But now for the answer. I had un-necessary "Do's" in the A and B Do-loops that I took out. That enabled to get rid of about 10 lines of code so less complicated. So it should be easier to understand now.
Thanks for the clarification! Yes, the code is pretty intelligible now.
John and I are in e-mail contact. Your code keeps evolving. If we rewrite your latest version in any other programming language, you’ll say that our version is a straw-man. And your code will keep changing, anyway. So what’s the point of putting any work into it now?
When you have a paper out, then it might be useful to react to it in public.
Re: Re: Coming Soon!
Posted: Thu Nov 18, 2021 9:42 am
by FrediFizzx
gill1109 wrote: ↑Thu Nov 18, 2021 5:32 am
John and I are in e-mail contact. Your code keeps evolving. If we rewrite your latest version in any other programming language, you’ll say that our version is a straw-man. And your code will keep changing, anyway. So what’s the point of putting any work into it now? ...
If you write the program in another language that is a faithful representation of the program, why the hell would I call it a straw-man? You guys are just procrastinating and copping out. If you change what the code does and is supposed to do, then for sure it will be a strawman.

.
Re: Coming Soon!
Posted: Sun Nov 21, 2021 9:13 am
by FrediFizzx
Yes, yes, yes, another freakin' update but this awesome 3-sphere quaternion simulation with 3D vectors just keeps getting better and better.

This one has a major update to the product calculation section. No more orientation lambda HV! No more imaginary components to have to cancel out. Perhaps Joy might explain a bit more about this major change. 6 million trials; one degree resolution. The trials for the product calculation are limited to 20,000 because that is all that is needed and more than that makes the PDF file huge. Check out that Meanq = 9.16956*10^-6! No imaginary components! And Meanq is just the average of -cos(
a -
b).

And..., that baby is still screaming
-a.b!
Plot Verification of the Analytical 3-Sphere Model Based on Geometric Algebra using Quaternions
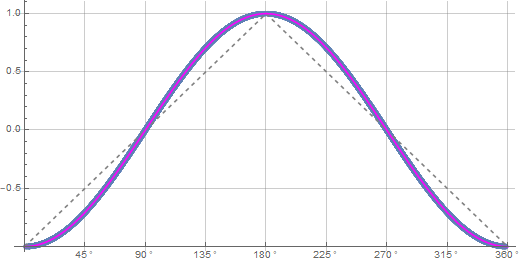 Blue is the data and magenta is the negative cosine curve for an exact match.
Blue is the data and magenta is the negative cosine curve for an exact match.
Cloud File.
https://www.wolframcloud.com/obj/fredif ... c-paper.nb
Direct Files.
download/newCS-37-S3quat-3D-new-prodcalc-paper.pdf
download/newCS-37-S3quat-3D-new-prodcalc-paper.nb
Enjoy!



.
Re: Re: Coming Soon!
Posted: Sun Nov 21, 2021 3:01 pm
by gill1109
Interesting. Especially the very last plot in the notebook file. Imagine running a smooth curve through those deviations. Between 0 and 90 degrees it would look like the sine of twice the angle. Starting at y = 0, curving up to height about y = 0.01 and then down, ending at y = 0. The next four segments of the curve do the same, first , mirrored in the x axis, then mirrored in the y-axis.
Re: Re: Coming Soon!
Posted: Sun Nov 21, 2021 4:31 pm
by FrediFizzx
gill1109 wrote: ↑Sun Nov 21, 2021 3:01 pm
Interesting. Especially the very last plot in the notebook file. Imagine running a smooth curve through those deviations. Between 0 and 90 degrees it would look like the sine of twice the angle. Starting at y = 0, curving up to height about y = 0.01 and then down, ending at y = 0. The next four segments of the curve do the same, first, mirrored in the x axis, then mirrored in the y-axis.
Hey! Guess what? No more orientation lambda HV! No more having to reverse the order to get rid of the cross-product imaginary components. Your 1/2 ab + 1/2 ba = ab or whatever it was, is gone for good!



.
Re: Re: Coming Soon!
Posted: Sun Nov 21, 2021 8:59 pm
by gill1109
FrediFizzx wrote: ↑Sun Nov 21, 2021 4:31 pm
gill1109 wrote: ↑Sun Nov 21, 2021 3:01 pm
Interesting. Especially the very last plot in the notebook file. Imagine running a smooth curve through those deviations. Between 0 and 90 degrees it would look like the sine of twice the angle. Starting at y = 0, curving up to height about y = 0.01 and then down, ending at y = 0. The next four segments of the curve do the same, first, mirrored in the x axis, then mirrored in the y-axis.
Hey! Guess what? No more orientation lambda HV! No more having to reverse the order to get rid of the cross-product imaginary components. Your 1/2 ab + 1/2 ba = ab or whatever it was, is gone for good!



Yes, I saw that, you just take the real part of ab instead. It means that the two negative cosine plots have little to do with one another.
Re: Re: Coming Soon!
Posted: Mon Nov 22, 2021 12:44 am
by Joy Christian
.
Dumb shall remain dumb. For that is their wont.

.
Re: Re: Coming Soon!
Posted: Mon Nov 22, 2021 5:19 am
by FrediFizzx
Joy Christian wrote: ↑Mon Nov 22, 2021 12:44 am
.
Dumb shall remain dumb. For that is their wont.

Ignorance is curable; stupid is forever.

.
Re: Re: Coming Soon!
Posted: Mon Nov 22, 2021 5:26 am
by FrediFizzx
gill1109 wrote: ↑Sun Nov 21, 2021 8:59 pm
FrediFizzx wrote: ↑Sun Nov 21, 2021 4:31 pm
gill1109 wrote: ↑Sun Nov 21, 2021 3:01 pm
Interesting. Especially the very last plot in the notebook file. Imagine running a smooth curve through those deviations. Between 0 and 90 degrees it would look like the sine of twice the angle. Starting at y = 0, curving up to height about y = 0.01 and then down, ending at y = 0. The next four segments of the curve do the same, first, mirrored in the x axis, then mirrored in the y-axis.
Hey! Guess what? No more orientation lambda HV! No more having to reverse the order to get rid of the cross-product imaginary components. Your 1/2 ab + 1/2 ba = ab or whatever it was, is gone for good!



Yes, I saw that, you just take the real part of ab instead. It means that the two negative cosine plots have little to do with one another.
In[123]:= q
Out[123]= Quaternion[0.240511, 0., 0., 0.]
There is only the real part. The rest nulled out by a process other than how it was being done before.
.
Re: Re: Coming Soon!
Posted: Mon Nov 22, 2021 8:05 am
by gill1109
FrediFizzx wrote: ↑Mon Nov 22, 2021 5:19 am
Joy Christian wrote: ↑Mon Nov 22, 2021 12:44 am
Dumb shall remain dumb. For that is their wont.

Ignorance is curable; stupid is forever.

Very true indeed!
Dumb is not knowing that there are important things that you don't know, even when they are pointed out to you. Dumb is relying on your vanity rather than being open to the possibility that maybe you got something wrong.
Re: Re: Coming Soon!
Posted: Mon Nov 22, 2021 8:10 am
by gill1109
FrediFizzx wrote: ↑Mon Nov 22, 2021 5:26 am
gill1109 wrote: ↑Sun Nov 21, 2021 8:59 pm
Yes, I saw that, you just take the real part of ab instead. It means that the two negative cosine plots have little to do with one another.
In[123]:= q
Out[123]= Quaternion[0.240511, 0., 0., 0.]
There is only the real part. The rest nulled out by a process other than how it was being done before.
Yes it is different from how you did it before, but itis not terribly transparent
Code: Select all
Do[r1[[i]]=({QA[[i]][[2]],QA[[i]][[3]],QA[[i]][[4]]});r2[[i]]=({QB[[i]][[2]],QB[[i]][[3]],QB[[i]][[4]]});
\[IndentingNewLine]QA1[[i]]=Flatten[{Re[QA[[i]]],r1[[i]]}].Qcoordinates2;
\[IndentingNewLine]QB1[[i]]=Flatten[{Re[QB[[i]]],r2[[i]]}].Qcoordinates2;
\[IndentingNewLine]QAB[[i]]=Re[QA1[[i]]**QB1[[i]]];
r0[[i]]=(Re[qa1[[i]]]Limit[Cross[\[Theta]3,bb1[[i]]],\[Theta]3->Sign[Re[qb1[[i]]]]bb1[[i]]]+Re[qb1[[i]]]Limit[Cross[aa1[[i]],\[Theta]4],\[Theta]4->Sign[Re[qa1[[i]]]]aa1[[i]]]-Limit[Cross[aa1[[i]],\[Theta]5],\[Theta]5->Sign[Re[qa1[[i]]]]aa1[[i]]]*Limit[Cross[\[Theta]6,bb1[[i]]],\[Theta]6->Sign[Re[qb1[[i]]]]bb1[[i]]])/
\[IndentingNewLine](Sin[ArcCos[aa1[[i]].bb1[[i]]]]);
\[IndentingNewLine]q={Re[QAB[[i]]],r0[[i]][[1]],r0[[i]][[2]],r0[[i]][[3]]}.Qcoordinates2;
\[IndentingNewLine]\[Phi]A=ArcTan[aa1[[i]][[1]],aa1[[i]][[2]]]/50;
\[IndentingNewLine]\[Phi]B=ArcTan[bb1[[i]][[2]],bb1[[i]][[1]]]/50;
\[IndentingNewLine]If[\[Phi]A*\[Phi]B>0,angle=ArcCos[aa1[[i]].bb1[[i]]]*180/\[Pi],angle=(2\[Pi]-ArcCos[aa1[[i]].bb1[[i]]])*180/\[Pi]];
\[IndentingNewLine]s=s+q[[1]];
\[IndentingNewLine]plotq[[i]]={angle,q[[1]]},{i,m3}]
Meanq=s/m; (*shows vanishing of the non-real part iJK*)
\[IndentingNewLine]Print["Meanq = ",Meanq]
\[IndentingNewLine]sim=ListPlot[plotq,PlotMarkers->{Automatic,Small},AspectRatio->8/16, Ticks->{{{0,0\[Degree]},{45,45\[Degree]},{90,90\[Degree]},{135,135\[Degree]},{180,180\[Degree]},{225,225\[Degree]},{270,270\[Degree]},{315,315\[Degree]},{360,360\[Degree]}},Automatic},GridLines->Automatic,AxesOrigin->{0,-1.0}];
\[IndentingNewLine]p1=Plot[-1+2x Degree/\[Pi],{x,0,180},PlotStyle->{Gray,Dashed}];
\[IndentingNewLine]p2=Plot[3-2x Degree/\[Pi],{x,180,360},PlotStyle->{Gray,Dashed}];
\[IndentingNewLine]negcos1=Plot[-Cos[x Degree],{x,0,360},PlotStyle->{Magenta}];
\[IndentingNewLine]Show[sim,p1,p2,negcos1]
Re: Re: Coming Soon!
Posted: Mon Nov 22, 2021 8:11 am
by Joy Christian
gill1109 wrote: ↑Mon Nov 22, 2021 8:05 am
Dumb is not knowing that there are important things that you don't know, even when they are pointed out to you. Dumb is relying on your vanity rather than being open to the possibility that maybe you got something wrong.
Very true indeed. The above description applies precisely to the retired statistician Richard D. Gill of Leiden University.

.
Re: Re: Coming Soon!
Posted: Mon Nov 22, 2021 8:29 am
by gill1109
Joy Christian wrote: ↑Mon Nov 22, 2021 8:11 am
gill1109 wrote: ↑Mon Nov 22, 2021 8:05 am
Dumb is not knowing that there are important things that you don't know, even when they are pointed out to you. Dumb is relying on your vanity rather than being open to the possibility that maybe you got something wrong.
Very true indeed. The above description applies precisely to the retired statistician Richard D. Gill of Leiden University.

Could be! Posterity may decide.



Re: Coming Soon!
Posted: Tue Nov 23, 2021 3:47 pm
by FrediFizzx
FrediFizzx wrote: ↑Sun Nov 21, 2021 9:13 am
Yes, yes, yes, another freakin' update but this awesome 3-sphere quaternion simulation with 3D vectors just keeps getting better and better.

This one has a major update to the product calculation section. No more orientation lambda HV! No more imaginary components to have to cancel out. Perhaps Joy might explain a bit more about this major change. 6 million trials; one degree resolution. The trials for the product calculation are limited to 20,000 because that is all that is needed and more than that makes the PDF file huge. Check out that Meanq = 9.16956*10^-6! No imaginary components! And Meanq is just the average of -cos(
a -
b).

And..., that baby is still screaming
-a.b!
Plot Verification of the Analytical 3-Sphere Model Based on Geometric Algebra using Quaternions
 Blue is the data and magenta is the negative cosine curve for an exact match.
Blue is the data and magenta is the negative cosine curve for an exact match.
Cloud File.
https://www.wolframcloud.com/obj/fredif ... c-paper.nb
Direct Files.
download/newCS-37-S3quat-3D-new-prodcalc-paper.pdf
download/newCS-37-S3quat-3D-new-prodcalc-paper.nb
Enjoy!



Found a tiny mistake that didn't affect the results so here is the fixed code.
Cloud File.
https://www.wolframcloud.com/obj/fredif ... c-forum.nb
Direct Files.
download/CS-39-S3quat-3D-new-prodcalc-forum.pdf
download/CS-39-S3quat-3D-new-prodcalc-forum.nb
Enjoy the fixed code! It is really awesome and just gets better and better.
.
Re: Re: Coming Soon!
Posted: Sat Nov 27, 2021 6:37 am
by gill1109
"Calculating Deviation from -Cosine Curve" shows a small systematic deviation. Your theory is never going to exactly reproduce the negative cosine.
Re: Re: Coming Soon!
Posted: Sat Nov 27, 2021 7:31 am
by FrediFizzx
gill1109 wrote: ↑Sat Nov 27, 2021 6:37 am
"Calculating Deviation from -Cosine Curve" shows a small systematic deviation. Your theory is never going to exactly reproduce the negative cosine.
 Blue is the data and magenta is the negative cosine curve for an exact match.
Blue is the data and magenta is the negative cosine curve for an exact match.



PS. Well, that is actually Joy's theory from 14 years ago! You should have gotten a big clue then.
.
Re: Re: Coming Soon!
Posted: Sat Nov 27, 2021 9:15 pm
by gill1109
Joy’s method delivers the cosine exactly. But I wouldn’t call it a theory. I think of it as science fantasy.
Re: Re: Coming Soon!
Posted: Sun Nov 28, 2021 2:17 am
by FrediFizzx
gill1109 wrote: ↑Sat Nov 27, 2021 9:15 pm
Joy’s method delivers the cosine exactly. But I wouldn’t call it a theory. I think of it as science fantasy.
Yep, Gill has had NO clue for 14 years that Bell's theory is junk physics so he lives in some kind of fantasyland all this time. I'm sorry, but it is time for you to get out of that fantasy and move on. Especially now that Joy has recently done away with your specific objections. There is now nothing left for you to cry about.

.
Re: Re: Coming Soon!
Posted: Sun Nov 28, 2021 4:43 am
by Joy Christian
gill1109 wrote: ↑Sat Nov 27, 2021 9:15 pm
Joy’s method delivers the cosine exactly. But I wouldn’t call it a theory. I think of it as science fantasy.
To those who lack originality and imagination, everything looks like fantasy.
.



