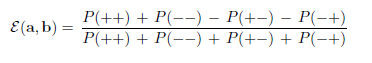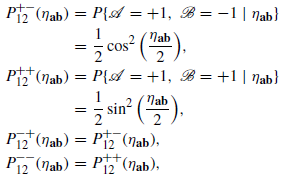Re: Coming Soon!
Posted: Thu Nov 04, 2021 8:24 pm
Ok, back to the original question. I think I need to do some slight fixin' on it.
) = 1/4, etc., does that prove that
= 1/4, etc., does that prove that 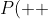 = \frac{1}{4} = \frac{1}{2}\sin^2 (\frac{\eta_{ab}}{2})) , etc. for our analytical situation? Keeping mind that P(++) and
, etc. for our analytical situation? Keeping mind that P(++) and ) , etc. are actually averages.
, etc. are actually averages.
______________________________________________________________________________________________________________________________
Ok, what we actually have here for the simulation is >\; =\; < \frac{1}{2}\sin^2 (\frac{\eta_{ab}}{2}) >\; = \frac{1}{4}) .
.
So, the question is actually this. Does,
 \; =\; \frac{1}{2}\sin^2 (\frac{\eta_{ab}}{2})) ??
??
Now the only way to equate those two would be by their totals or length of the lists. So, let's see. For a million trials, there are 250,000 events that are (++). and there are 250,000 events that are) which makes sense since basically there would be a 1/4 each of the sin^2 and cos^2 probabilities. So, they match quantity-wise. But what we are actually trying to find out is this,
which makes sense since basically there would be a 1/4 each of the sin^2 and cos^2 probabilities. So, they match quantity-wise. But what we are actually trying to find out is this,
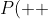 \; =\; \frac{1}{2}\sin^2 (\frac{\eta_{ab}}{2})) . Is that true for our simulation? Now, we know that the probability of getting (++) for the simulation is 1/4 so
. Is that true for our simulation? Now, we know that the probability of getting (++) for the simulation is 1/4 so
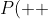 \; =\; \frac{1}{4})
Now, we also know the average of getting,
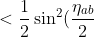 >\;=\;\frac{1}{4})
So,
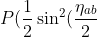)\;=\;\frac{1}{4})
Then by virtue of what QM says about it, I think we can say that,
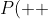 \; =\; \frac{1}{2}\sin^2 (\frac{\eta_{ab}}{2})) for both the simulation and the analytical formulas. But maybe more proof is needed?
for both the simulation and the analytical formulas. But maybe more proof is needed?
.
Ok, now a question. Since all P(++)'s, etc. are equal to a 1/4 and the average ofFrediFizzx wrote:Ok, now for the next part of this.FrediFizzx wrote:This expression seems a bit odd to me.
In order to get the probabilities for each of the four outcome pairs say in a large simulation, they first have to be averaged over many trials per (a-b) angle. It seems to me that in a proper simulation each of the four probabilities are going to converge to 1/4 for very large number of trials. At least that is what I am finding with our latest simulation.
Ave ++ = 0.248903
Ave -- = 0.248803
Ave +- = 0.246508
Ave -+ = 0.255786
That was for 10,000 trials. For 5 million trials,
Ave ++ = 0.249787
Ave -- = 0.249991
Ave +- = 0.250293
Ave -+ = 0.249929
Much closer to 1/4 each. So, for analytical purposes, it doesn't seem unreasonable to assign 1/4 to each of the four outcome pair probabilities.
QM assigns for those 4 outcome probabilities,
Again, in a simulation with many trials, we have to averageand
over all the (a-b) angles. Lo and behold, when we do that we obtain,
,
,
Because.
So, it seems to me that all of the parts of the original E(a, b) expression are all equal to 1/4. Analytically-wise.
______________________________________________________________________________________________________________________________
Ok, what we actually have here for the simulation is
So, the question is actually this. Does,
Now the only way to equate those two would be by their totals or length of the lists. So, let's see. For a million trials, there are 250,000 events that are (++). and there are 250,000 events that are
Now, we also know the average of getting,
So,
Then by virtue of what QM says about it, I think we can say that,
.